题目内容
（04年全国卷III理）（14分）
已知数列{an}的前n项和Sn满足：Sn=2an +(-1)n,n≥1.
⑴写出数列{an}的前3项a1,a2,a3；
⑵求数列{an}的通项公式；
⑶证明：对任意的整数m>4，有
.
解析：⑴当n=1时,有：S1=a1=2a1+(-1)
a1=1；
当n=2时,有：S2=a1+a2=2a2+(-1)2a2=0；
当n=3时,有：S3=a1+a2+a3=2a3+(-1)3a3=2；
综上可知a1=1,a2=0,a3=2；
⑵由已知得：
化简得：
上式可化为：
故数列{
}是以
为首项, 公比为2的等比数列.
故
∴
数列{
}的通项公式为：
.
⑶由已知得：
.
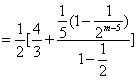
故
( m>4).
练习册系列答案
阅读快车系列答案
相关题目
，求AC与侧面PBC所成角的大小．
，求侧面PBC与侧面PAC所成二面角的大小．