题目内容
设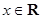 ,函数
,函数 ,
, .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若 ,求
,求 的值.
的值.
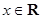 ,函数
,函数 ,
, .
.(1)求函数
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(2)若
 ,求
,求 的值.
的值.(1)周期为 ,单调递增区间是
,单调递增区间是 (
( );(2)
);(2) .
.
 ,单调递增区间是
,单调递增区间是 (
( );(2)
);(2) .
.试题分析:(1)首先三角函数的问题必须把函数化为
 的形式,才能应用正弦函数的知识解决问题,本题中
的形式,才能应用正弦函数的知识解决问题,本题中



 ;(2)本题中已知条件要化简,待求值的式子也要化简,已知为
;(2)本题中已知条件要化简,待求值的式子也要化简,已知为 ,即为
,即为

 ,问题变成已知
,问题变成已知 ,求一个式子的值,这个式子一般是关于
,求一个式子的值,这个式子一般是关于 的齐次式,分子分母同时除以
的齐次式,分子分母同时除以 的幂可化为
的幂可化为 的式子,当然也可直接把
的式子,当然也可直接把 用
用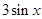 代入化简得出结论,如
代入化简得出结论,如 .
.试题解析:(1)
 (1分)
(1分) , (2分)
, (2分)所以,函数
 的最小正周期为
的最小正周期为 . (2分)
. (2分)由
 (
( ),得
),得 (
( ),(2分)
),(2分)所以函数
 的单调递增区间是
的单调递增区间是 (
( ). (1分)
). (1分)(2)由题意,
 ,
, , (1分)
, (1分)所以,
 . (1分)
. (1分)所以,

 . (4分)
. (4分)(中间步骤每步1分,答案2分)

练习册系列答案
相关题目
 .
. 的单调增区间;
的单调增区间; ,
, 求b+c的值.
求b+c的值.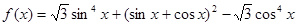 .
.
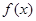 的最小值及取最小值时
的最小值及取最小值时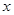 的集合;
的集合;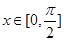 时的值域;
时的值域;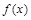 在区间
在区间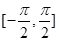 上的图像(要求列表,描点).
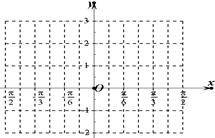
上的图像(要求列表,描点). 的图像如右图所示,则
的图像如右图所示,则 .
.
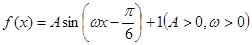 的最大值为
的最大值为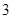 ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为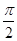 .
.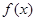 的解析式;
的解析式;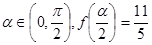 ,求
,求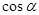 的值.
的值.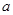 是实数,则函数
是实数,则函数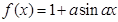 的图象可能是( )
的图象可能是( )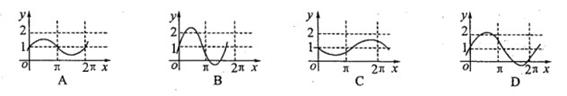
 ,
, 的最小正周期为( )
的最小正周期为( )



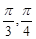 ]上单调递增,则ω的取值范围是_________.
]上单调递增,则ω的取值范围是_________.
 ,且其图像关于直线
,且其图像关于直线 对称,则( )
对称,则( ) 的最小正周期为
的最小正周期为 ,且在
,且在 上为增函数
上为增函数 ,且在
,且在 上为增函数
上为增函数