题目内容
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
频数 | 8 | 20 | 42 | 22 | 8 |
B配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y= 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
(1)0.3,0.42(2)X的分布列为
X | -2 | 2 | 4 |
P | 0.04 | 0.54 | 0.42 |
E(X)=2.68.
【解析】(1)由试验结果知,用A配方生产的产品中优质品的频率为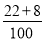 =0.3,所以用A配方生产的产品的优质品率的估计值为0.3.由试验结果知,用B配方生产的产品中优质品的频率为
=0.3,所以用A配方生产的产品的优质品率的估计值为0.3.由试验结果知,用B配方生产的产品中优质品的频率为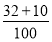 =0.42,所以用B配方生产的产品的优质品率的估计值为0.42.
=0.42,所以用B配方生产的产品的优质品率的估计值为0.42.
(2)用B配方生产的100件产品中,其质量指标值落入区间[90,94),[94,102),[102,110)的频率分别为0.04,0.54,0.42,因此P(X=-2)=0.04,P(X=2)=0.54,P(X=4)=0.42,
即X的分布列为
X | -2 | 2 | 4 |
P | 0.04 | 0.54 | 0.42 |
X的数学期望E(X)=-2×0.04+2×0.54+4×0.42=2.68.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目









