题目内容
已知函数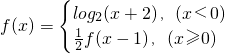 ,若y=f(x)与
,若y=f(x)与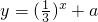 的图象有三个不同交点,则实数a的取值范围是
的图象有三个不同交点,则实数a的取值范围是
- A.
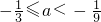
- B.
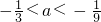
- C.
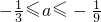
- D.
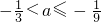
A
分析:作出函数的图象,由y=f(x)与y=( )x+a的图象有三个不同交点,根据函数的图象,即可确定实数a的取值范围.
)x+a的图象有三个不同交点,根据函数的图象,即可确定实数a的取值范围.
解答: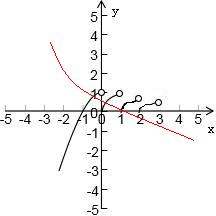 解:函数
解:函数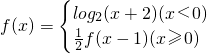 ,图象如图所示,
,图象如图所示,
f(x)=( )x+a可由f(x)=(
)x+a可由f(x)=( )x变换得到,由图象可知,f(x)=(
)x变换得到,由图象可知,f(x)=( )x+a图象经过(1,0)时,有三个交点,此时a=-
)x+a图象经过(1,0)时,有三个交点,此时a=- ;
;
经过(2,0)时,有四个交点,此时a=- ,
,
根据图象,y=f(x)与y=( )x+a的图象有三个不同交点时,实数a的取值范围是-
)x+a的图象有三个不同交点时,实数a的取值范围是- ≤a<-
≤a<- .
.
故选A.
点评:本题考查函数图象交点的个数问题,考查数形结合的数学思想,正确作出函数的图象是关键.
分析:作出函数的图象,由y=f(x)与y=(
 )x+a的图象有三个不同交点,根据函数的图象,即可确定实数a的取值范围.
)x+a的图象有三个不同交点,根据函数的图象,即可确定实数a的取值范围.解答:
 解:函数
解:函数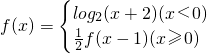 ,图象如图所示,
,图象如图所示,f(x)=(
 )x+a可由f(x)=(
)x+a可由f(x)=( )x变换得到,由图象可知,f(x)=(
)x变换得到,由图象可知,f(x)=( )x+a图象经过(1,0)时,有三个交点,此时a=-
)x+a图象经过(1,0)时,有三个交点,此时a=- ;
;经过(2,0)时,有四个交点,此时a=-
 ,
,根据图象,y=f(x)与y=(
 )x+a的图象有三个不同交点时,实数a的取值范围是-
)x+a的图象有三个不同交点时,实数a的取值范围是- ≤a<-
≤a<- .
.故选A.
点评:本题考查函数图象交点的个数问题,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
相关题目
 ,若y=f(x)与
,若y=f(x)与 的图象有三个不同交点,则实数a的取值范围是( )
的图象有三个不同交点,则实数a的取值范围是( )



 ,若y=f(x)图象上的点
,若y=f(x)图象上的点 处的切线斜率为-4,求y=f(x)的极大、极小值.
处的切线斜率为-4,求y=f(x)的极大、极小值.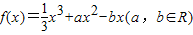 ,若y=f(x)图象上的点
,若y=f(x)图象上的点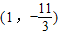 处的切线斜率为-4,求y=f(x)的极大、极小值.
处的切线斜率为-4,求y=f(x)的极大、极小值.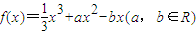 ,若y=f(x)图象上的点
,若y=f(x)图象上的点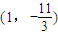 处的切线斜率为-4,求y=f(x)的极大、极小值.
处的切线斜率为-4,求y=f(x)的极大、极小值.