题目内容
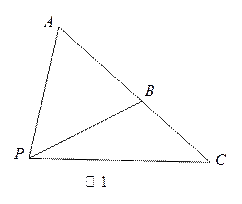
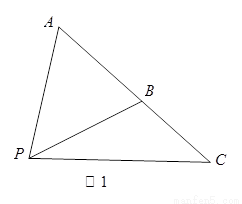
(Ⅰ)如图1,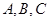 是平面内的三个点,且
是平面内的三个点,且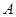 与
与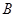 不重合,
不重合,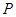 是平面内任意一点,若点
是平面内任意一点,若点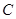 在直线
在直线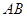 上,试证明:存在实数
上,试证明:存在实数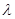 ,使得:
,使得: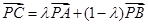 .
.
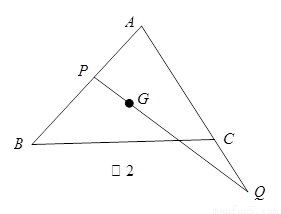
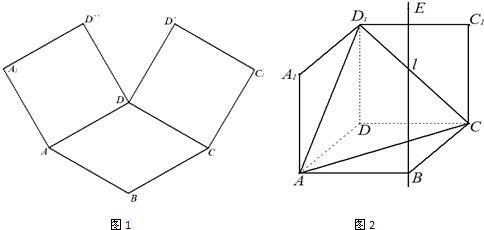
(Ⅱ)如图2,设 为
为 的重心,
的重心, 过
过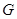 点且与
点且与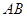 、
、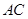 (或其延长线)分别交于
(或其延长线)分别交于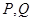 点,若
点,若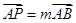 ,
,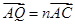 ,试探究:
,试探究: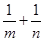 的值是否为定值,若为定值,求出这个
的值是否为定值,若为定值,求出这个
定值;若不是定值,请说明理由.
【答案】
解:(Ⅰ)由于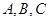 三点共线,所以存在实数
三点共线,所以存在实数 使得:
使得:
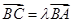 ,
………2分
,
………2分
即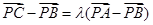 ………4分
………4分
化简为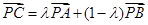
结论得证. ………6分
(Ⅱ)连结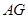 ,因为
,因为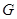 为
为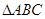 的重心,
的重心,
所以: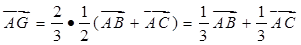 ………8分
………8分
又因为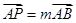 ,
,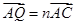
所以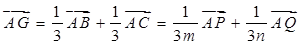 ………10分
………10分
由(Ⅰ)知: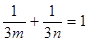 所以
所以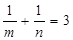 为定值.…12分
为定值.…12分
【解析】略

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).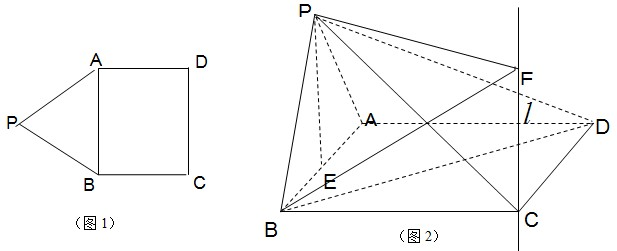
 ,
,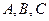 是平面内的三个点,且
是平面内的三个点,且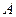 与
与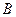 不重合,
不重合, 是平面内任意一点,若点
是平面内任意一点,若点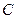 在直线
在直线 上,试证明:存在实数
上,试证明:存在实数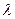 ,使得:
,使得: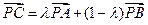 .
.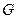 为
为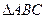 的重心,
的重心,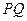 过
过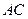 (或其延长线)分别交于
(或其延长线)分别交于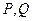 点,若
点,若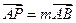 ,
, ,试探究:
,试探究: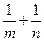 的值是否为定值,若为定值,求出这个
的值是否为定值,若为定值,求出这个