题目内容
在区间[-2,2]上随机取一个数x,cos
的值介于[0,
]之间的概率为( )
| πx |
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题考查的知识点是几何概型,关键是要找出cos
πx的值介于0到0.5之间对应线段的长度,再将其代入几何概型计算公式进行求解.
| 1 |
| 3 |
解答:解:在区间[-2,2]上随机取一个数x,
即x∈[-2,2]时,要使cos
πx的值介于0到0.5之间,
需使
≤
πx≤
或使-
≤
πx≤-
∴1≤x≤
,或-
≤x≤-1,它们区间长度为 1,
由几何概型知 cos
πx的值介于0到0.5之间的概率为
.
故选C.
即x∈[-2,2]时,要使cos
| 1 |
| 3 |
需使
| π |
| 3 |
| 1 |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
∴1≤x≤
| 3 |
| 2 |
| 3 |
| 2 |
由几何概型知 cos
| 1 |
| 3 |
| 1 |
| 4 |
故选C.
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
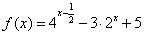 在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值;
在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值;  在区间[-2,2]上的最大值为14,求实数a的值。
在区间[-2,2]上的最大值为14,求实数a的值。