[题目]已知椭圆上任意一点到两焦点距离之和为.离心率为．(1)求椭圆的标准方程,(2)若直线的斜率为.直线与椭圆C交于两点．点为椭圆上一点.求的面积的最大值．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆上任意一点到两焦点距离之和为，离心率为．

（1）求椭圆的标准方程；

（2）若直线的斜率为，直线与椭圆C交于两点．点为椭圆上一点，求的面积的最大值．

【答案】（1）；（2）2

【解析】

试题分析：（1）由椭圆定义，椭圆上任意一点到两焦点距离之和为常数，又因为，从而求得即可得椭圆的标准方程；（2）设的方程为，把其与椭圆的方程联立，求出弦长为△PAB的底，由点线距离公式求出△PAB的高，，表示出三角形的面积，然后用基本不等式求最值即可

试题解析：（1）由条件得：，解得，所以椭圆的方程为

（2）设的方程为，点

由消去得．

令，解得，由韦达定理得．

则由弦长公式得．

又点P到直线的距离，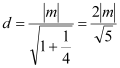

∴，

当且仅当，即时取得最大值．∴△PAB面积的最大值为2．

练习册系列答案

学优冲刺100系列答案

名校秘题小学毕业升学系统总复习系列答案

相关题目

【题目】设函数f(x)=ax2–a–lnx，g(x)=，其中a∈R，e=2.718…为自然对数的底数.

（1）讨论f(x) 的单调性；

（2）证明：当x＞1时，g(x)＞0；

（3）如果f(x)＞g(x) 在区间（1，+∞）内恒成立，求实数a的取值范围.

【题目】已知抛物线的方程为，过点（为常数）作抛物线的两条切线，切点分别为，.

（1）过焦点且在轴上截距为的直线与抛物线交于，两点，，两点在轴上的射影分别为，，且，求抛物线的方程；

（2）设直线，的斜率分别为，.求证：为定值.

【题目】已知二次函数满足，且方程有两个相等的实数根

（1）求函数的解析式;

（2）若是上的奇函数，且时，，求的解析式;

（3）若不等式对一切实数，恒成立，求实数的取值范围.

【题目】中国古代十进制的算筹计数法，在世界数学史上是一个伟大的创造. 算筹实际上是一根根同样长短的小木棍，用算筹表示数1～9的方法如图:例如：163可表示为“”，27可表示为“”.现有6根算筹，用来表示不能被10整除的两位数，算筹必须用完，则这样的两位数的个数为_________.

【题目】如图，直三棱柱中，，，，为的中点，点为线段上的一点.

（1）若，求证：；

（2）若，异面直线与所成的角为，求直线与平面所成角的正弦值.

【题目】甲、乙两所学校进行同一门课程的考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下列联表：

班级与成绩列联表

	优秀	不优秀	总计
甲队	80	40	120
乙队	240	200	240
合计	320	240	560

（1）能否在犯错误的概率不超过0.025的前提下认为成绩与学校有关系；

（2）采用分层抽样的方法在两所学校成绩优秀的320名学生中抽取16名同学．现从这16名同学中随机抽取3名运同学作为成绩优秀学生代表介绍学习经验，记这3名同学来自甲学校的人数为，求的分布列与数学期望．附：

参考数据：

，其中.

【题目】某公司计划在报刊与网络媒体上共投放30万元的广告费，根据计划，报刊与网络媒体至少要投资4万元．根据市场前期调研可知，在报刊上投放广告的收益与广告费满足，在网络媒体上投放广告的收益与广告费满足，设在报刊上投放的广告费为(单位：万元)，总收益为(单位：万元).

(1)当在报刊上投放的广告费是18万元时，求此时公司总收益；

(2)试问如何安排报刊、网络媒体的广告投资费，才能使总收益最大?

【题目】已知倾斜角为的直线经过抛物线：的焦点，与抛物线相交于、两点，且.

（Ⅰ）求抛物线的方程；

（Ⅱ）过点的两条直线、分别交抛物线于点、和、，线段和的中点分别为、.如果直线与的倾斜角互余，求证：直线经过一定点.

试题分类