题目内容
双曲线M的中心在原点,并以椭圆
+
=1的焦点为焦点,以抛物线y2=-2
x的准线为右准线.
(1)求双曲线M的方程;
(2)设直线l:y=kx+3与双曲线M相交于A、B两点,O是原点.求k值,使
•
=0.
| x2 |
| 25 |
| y2 |
| 13 |
| 3 |
(1)求双曲线M的方程;
(2)设直线l:y=kx+3与双曲线M相交于A、B两点,O是原点.求k值,使
| OA |
| OB |
分析:(1)由题意可得所求的双曲线的半焦距 c=2
,准线为:x=
从而可得
=
,可求双曲线M的方程
(2)设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、联立方程组
消去y(k2-3)x2+6kx+18=0,设A(x1,y1)B(x2,y2)、则k2-3≠0,△=36k2-4(k2-3)×18>0,解可得,-
<k<
,从而有 x1+x2=-
,x1x2=
,由
•
=0,则有x1x2+y1y2=0,可求k.
| 3 |
| ||
| 2 |
| a2 |
| c |
| ||
| 2 |
(2)设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、联立方程组
|
| 6 |
| 6 |
| 6k |
| k2-3 |
| 18 |
| k2-3 |
| OA |
| OB |
解答:解:(1)由题设知,椭圆
+
=1的半焦距为:c=2
,…..(1分)
又抛物线y2=-2
x的准线为:x=
.…..(2分)
设双曲线M的方程为
-
=1,依题意有
=
,…..(3分)
故a2=
c=
•2
=3,又b2=c2-a2=12-3=9.…..(4分)
∴双曲线M的方程为
-
=1.…..(5分)
(2)设直线l与双曲线M的交点为A(x1,y1)、B(x2,y2)两点
联立方程组
消去y得 (k2-3)x2+6k+18=0,…..(7分)
∵A(x1,y1)、B(x2,y2)两点的横坐标是上述方程的两个不同实根,
∴k2-3≠0…..(8分)
∴△=(6k)2-4(k2-3)×18>0? -
<k<
,从而有
x1+x2=-
,x1x2=
.…(9分)
又y1=kx1+3,y2=kx2+3
∴y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9=
-
+9=9
…..…..(11分)
若
•
=0,则有 x1x2+y1y2=0,即
+9=0⇒k2=1⇒k=±1.
∴当k=±1时,使得
•
=0.…..(13分)
| x2 |
| 25 |
| y2 |
| 13 |
| 3 |
又抛物线y2=-2
| 3 |
| ||
| 2 |
设双曲线M的方程为
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| ||
| 2 |
故a2=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴双曲线M的方程为
| x2 |
| 3 |
| y2 |
| 9 |
(2)设直线l与双曲线M的交点为A(x1,y1)、B(x2,y2)两点
联立方程组
|
∵A(x1,y1)、B(x2,y2)两点的横坐标是上述方程的两个不同实根,
∴k2-3≠0…..(8分)
∴△=(6k)2-4(k2-3)×18>0? -
| 6 |
| 6 |
x1+x2=-
| 6k |
| k2-3 |
| 18 |
| k2-3 |
又y1=kx1+3,y2=kx2+3
∴y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9=
| 18k2 |
| k2-3 |
| 18k2 |
| k2-3 |
…..…..(11分)
若
| OA |
| OB |
| 18 |
| k2-3 |
∴当k=±1时,使得
| OA |
| OB |
点评:本题主要考查了由双曲线的性质求解双曲线的方程及直线与曲线的位置关系,要求考生具备一定的逻辑推理与计算的能力,本题具有较大的综合性.本题的易错点是混淆椭圆、双曲线、抛物线的性质.

练习册系列答案
相关题目
 +
+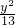 =1的焦点为焦点,以抛物线y2=-2
=1的焦点为焦点,以抛物线y2=-2 x的准线为右准线.
x的准线为右准线. •
• =0?
=0?