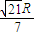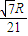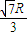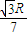题目内容
已知半径为R的得球面上有三点A，B，C，已知AB，AC之间球面距离都是
，BC间的球面距离为
，过A，B，C三点作球的截面，则球心到此截面的距离为（ ）
| πR |
| 2 |
| πR |
| 3 |
分析：根据球面距离的定义先求出∠AOB、∠BOC的大小，欲求球心O到截面ABC的距离，可设截面圆的圆心为O1，可通过解直角三角形AOO1解决．
解答：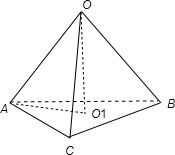
解：如图，因为球O的半径为R，B、C两点间的球面距离为
，
点A与B、C两点间的球面距离均为
，所以∠BOC=
，∠AOB=∠AOC=
．
∴BC=R，AC=AB=
R，
∴由余弦定理得cos∠BAC=
=
，
∴sin∠BAC
，
设截面圆的圆心为O1，连接AO1，
则截面圆的半径R=AO1，由正弦定理得r=
=
=
R，
所以OO1=
=
=
．
故选A．
解：如图，因为球O的半径为R，B、C两点间的球面距离为| πR |
| 3 |
点A与B、C两点间的球面距离均为
| πR |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴BC=R，AC=AB=
| 2 |
∴由余弦定理得cos∠BAC=
| 2R2+2R2-R2 |
| 2×2R×R |
| 3 |
| 4 |
∴sin∠BAC
| ||
| 4 |
设截面圆的圆心为O1，连接AO1，
则截面圆的半径R=AO1，由正弦定理得r=
| BC |
| 2sin∠BAC |
| R | ||||
2×
|
2
| ||
| 7 |
所以OO1=
| OA2-r2 |
R2-(
|
| ||
| 7 |
故选A．
点评：本题主要考查了球的性质、正弦定理解三角形以及点面间的距离计算，属于中档题．
练习册系列答案
相关题目
，BC间的球面距离为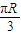
，过A，B，C三点作球的截面，则球心到此截面的距离为（ ）
