题目内容
设函数f(x)=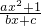 是奇函数,其中a,b,c∈N,f(1)=2,f(2)<3.
是奇函数,其中a,b,c∈N,f(1)=2,f(2)<3.
(Ⅰ)求a,b,c的值;
(Ⅱ)判断并证明f(x)在(-∞,-1]上的单调性.
解:(Ⅰ)由f(x)=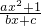 是奇函数得:f(-x)+f(x)=0,∴
是奇函数得:f(-x)+f(x)=0,∴ ,∴
,∴ ,
,
解得 c=0,即 .
.
又f(1)=2,∴ .
.
又 f(2)<3,可得 ,
, ,∴-1<a<2,
,∴-1<a<2,
∵a∈N,∴a=0或1.
若a=0,则 (舍去),∴a=b=1,c=0.
(舍去),∴a=b=1,c=0.
(Ⅱ)由(Ⅰ)知,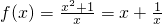 ,f(x)在(-∞,-1]上单调递增.
,f(x)在(-∞,-1]上单调递增.
下用定义证明:设x1<x2≤-1,则:f(x1)-f(x2)= =
= =
= ,
,
因为x1<x2≤-1,x1-x2<0, ,
,
∴f(x1)-f(x2)<0,故f(x)在(-∞,-1]上单调递增.
分析:(Ⅰ)由f(-x)+f(x)=0,求得 c=0,即 .再由f(1)=2、f(2)<3,a∈N,求得a,b,的值,从而得到a,b,c的值.
.再由f(1)=2、f(2)<3,a∈N,求得a,b,的值,从而得到a,b,c的值.
(Ⅱ)由(Ⅰ)知,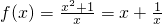 ,f(x)在(-∞,-1]上单调递增.设x1<x2≤-1,则由f(x1)-f(x2)=
,f(x)在(-∞,-1]上单调递增.设x1<x2≤-1,则由f(x1)-f(x2)= <0,从而得到 f(x)
<0,从而得到 f(x)
在(-∞,-1]上单调递增.
点评:本题主要考查函数的奇偶性的应用,用函数的单调性的定义证明函数的单调性,属于基础题.
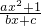 是奇函数得:f(-x)+f(x)=0,∴
是奇函数得:f(-x)+f(x)=0,∴ ,∴
,∴ ,
,解得 c=0,即
 .
.又f(1)=2,∴
 .
.又 f(2)<3,可得
 ,
, ,∴-1<a<2,
,∴-1<a<2,∵a∈N,∴a=0或1.
若a=0,则
 (舍去),∴a=b=1,c=0.
(舍去),∴a=b=1,c=0.(Ⅱ)由(Ⅰ)知,
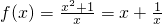 ,f(x)在(-∞,-1]上单调递增.
,f(x)在(-∞,-1]上单调递增.下用定义证明:设x1<x2≤-1,则:f(x1)-f(x2)=
 =
= =
= ,
,因为x1<x2≤-1,x1-x2<0,
 ,
,∴f(x1)-f(x2)<0,故f(x)在(-∞,-1]上单调递增.
分析:(Ⅰ)由f(-x)+f(x)=0,求得 c=0,即
 .再由f(1)=2、f(2)<3,a∈N,求得a,b,的值,从而得到a,b,c的值.
.再由f(1)=2、f(2)<3,a∈N,求得a,b,的值,从而得到a,b,c的值.(Ⅱ)由(Ⅰ)知,
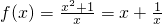 ,f(x)在(-∞,-1]上单调递增.设x1<x2≤-1,则由f(x1)-f(x2)=
,f(x)在(-∞,-1]上单调递增.设x1<x2≤-1,则由f(x1)-f(x2)= <0,从而得到 f(x)
<0,从而得到 f(x)在(-∞,-1]上单调递增.
点评:本题主要考查函数的奇偶性的应用,用函数的单调性的定义证明函数的单调性,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 (m、n为常数,且m∈R+,n∈R).
(m、n为常数,且m∈R+,n∈R).