题目内容
设函数f(x)=e2x+|ex-a|,(a为实数,x∈R).
(1)求证:函数f(x)不是奇函数;
(2)若g(x)=xa在(0,+∞)单调减,求满足不等式f(x)>a2的x的取值范围;
(3)求函数f(x)的值域(用a表示).
(1)求证:函数f(x)不是奇函数;
(2)若g(x)=xa在(0,+∞)单调减,求满足不等式f(x)>a2的x的取值范围;
(3)求函数f(x)的值域(用a表示).
分析:(1)利用反证法,假设f(x)是奇函数,则f(-x)=-f(x),推出矛盾结果,即可证明函数f(x)不是奇函数;
(2)利用g(x)=xa在(0,+∞)单调减,求出a的范围,然后解不等式f(x)>a2,求出x的取值范围;
(3)通过当a≤0,0≤a≤
,a≥
,分别求函数f(x)的值域(用a表示)即可.
(2)利用g(x)=xa在(0,+∞)单调减,求出a的范围,然后解不等式f(x)>a2,求出x的取值范围;
(3)通过当a≤0,0≤a≤
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)证明:假设f(x)是奇函数,则f(-x)=-f(x),
而x∈R,则f(0)=0,而f(0)=e0+|e0-a|=1+|1-a|≠0,故假设不成立,
从而函数f(x)不是奇函数.
(2)因g(x)=xa在(0,+∞)单调减,
则a<0,e2x+|ex-a|=e2x+ex-a>a2
则(ex-a)(ex+a+1)>0,
而(ex-a)>0,则ex>-a-1,
于是x>ln[-(a+1)];
(3)设ex=t,则t>0,y=f(x)=t2+|t-a|,
当a≤0时,y=f(x)=t2+t-a在t>0时单调增,则f(x)>f(0)=-a;
当0≤a≤
时,y=f(x)=t2+t-a≥f(a)=a2;
当a≥
时,y=f(x)=t2+t-a≥f(
)=a-
;
故当a≤0时,f(x)的值域为(-a,+∞);
当0≤a≤
时,f(x)的值域为(a2,+∞);
当a≥
时,f(x)的值域为(a-
,+∞).
而x∈R,则f(0)=0,而f(0)=e0+|e0-a|=1+|1-a|≠0,故假设不成立,
从而函数f(x)不是奇函数.
(2)因g(x)=xa在(0,+∞)单调减,
则a<0,e2x+|ex-a|=e2x+ex-a>a2
则(ex-a)(ex+a+1)>0,
而(ex-a)>0,则ex>-a-1,
于是x>ln[-(a+1)];
(3)设ex=t,则t>0,y=f(x)=t2+|t-a|,
当a≤0时,y=f(x)=t2+t-a在t>0时单调增,则f(x)>f(0)=-a;
当0≤a≤
| 1 |
| 2 |
当a≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故当a≤0时,f(x)的值域为(-a,+∞);
当0≤a≤
| 1 |
| 2 |
当a≥
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查函数的单调性的应用,函数的值域的求法,分类讨论思想的应用,考查转化思想计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
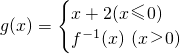 ,则g[g(-1)]=________.
,则g[g(-1)]=________.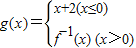 ,则g[g(-1)]= .
,则g[g(-1)]= .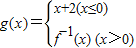 ,则g[g(-1)]= .
,则g[g(-1)]= .