题目内容
等差数列{an}和{bn}的前n项和分别为Sn和Tn,且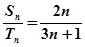 ,则
,则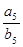 ( )
( )
A.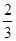 | B.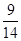 | C.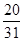 | D.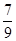 |
B
解析试题分析:由于等差数列{an}和{bn}的前n项和分别为Sn和Tn,那么根据等差数列的中项性质可知,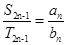 ,因此可知
,因此可知 ,故选B.
,故选B.
考点:等差数列的求和
点评:解决该试题的关键是利用等差中项的性质得到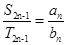 ,属于基础题。要熟练的掌握并计算。
,属于基础题。要熟练的掌握并计算。

练习册系列答案
相关题目
在等差数列{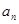 }中,a1>0,
}中,a1>0, 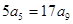 , 则数列{
, 则数列{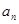 }前n项和
}前n项和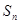 取最大
取最大
值时,n的值等( )
| A.12 | B.11 | C.10 | D.9 |
等差数列-5,-2,1,…的前20项的和为( )
| A.450 | B.470 | C.490 | D.510 |
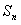 是等差数列
是等差数列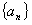 的前
的前 项和,若
项和,若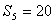 ,则
,则 ( )
( )
| A.15 | B.18 | C.9 | D.12 |
已知等差数列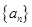 的前项和为
的前项和为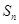 ,且
,且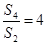 ,则
,则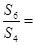 ( )
( )
A.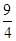 | B.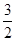 | C.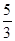 | D.4 |
设等差数列 的前n项和为
的前n项和为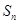 ,若
,若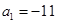 ,
, ,则当
,则当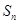 取最小值时,n等于( )
取最小值时,n等于( )
| A.6 | B.7 | C.8 | D.9 |
等差数列{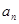 }中,
}中,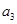 =2,
=2,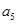 =7,则
=7,则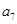 =
=
| A.10 | B.20 | C.16 | D.12 |
已知数列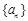 是公比为q的等比数列,且
是公比为q的等比数列,且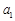 ,
,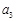 ,
,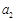 成等差数列,则q=
成等差数列,则q=
A.1或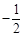 | B.1 | C.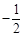 | D.-2 |
设数列 的前n项和为
的前n项和为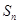 ,令
,令 ,称
,称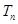 为数列
为数列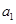 ,
,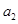 ,……,
,……,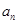 的“理想数”,已知数列
的“理想数”,已知数列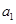 ,
,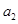 ,……,
,……,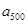 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 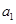 ,
,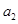 ,……,
,……,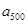 的“理想数”为( )
的“理想数”为( )
| A.2002 | B.2004 | C.2006 | D.2008 |