题目内容
已知10只狗的血球体积及红血球数的测量值如下表:血球体积x/mm | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
红血球数y/百万 | 6.53 | 6.30 | 9.52 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 8.72 |
(1)画出散点图;
(2)求回归直线方程.
解析:本例实际上通过数值计算例子,说明在散点图上,回归直线使 解:(1)散点图如下: (2) 设回归直线的方程为 a= 所以所求的回归直线为
达到最小值,其中a、b是任意直线的斜率和截距.
=
(45+42+46+48+42+35+58+40+39+50)=44.50,
=
(6.53+6.30+9.52+7.50+6.99+5.90+9.49+6.20+6.55+8.72)=7.37,
=a
+b,则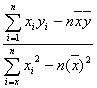
=0.175,b=
-a
=-0.42,
=0.175x-0.42. 
王立博探究学案系列答案
口算100系列答案
完全作业系列答案
春雨教育默写高手系列答案
高分装备复习与测试系列答案
全效学习同步学练测系列答案
高效课堂导学案吉林出版集团有限责任公司系列答案
自我评价与提升系列答案
我为题狂系列答案
| x | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
| y | 6.53 | 6.30 | 9.25 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 7.72 |
（1）画出上表的散点图；
（2）求出回归直线并且画出图形
（3）回归直线必经过的一点是哪一点？
X | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
y | 6.35 | 6.30 | 9.25 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 7.72 |
其中ｘ为（血球体积，mm），ｙ为（血红球数，百万）
（1）画出上表的散点图;
（2）求出回归直线并且画出图形;
血球体积ｘ（ｍｍ） | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
红血球数ｙ（百万） | 6.53 | 6.30 | 9.52 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 8.72 |
若已知二者相关，求出回归直线方程.
已知10只狗的血球体积及红血球的测量值如下
|
|
|
| 45 | 6.53 |
| 42 | 6.30 |
| 46 | 9.25 |
| 48 | 7.50 |
| 42 | 6.99 |
| 35 | 5.90 |
| 58 | 9.49 |
| 40 | 6.20 |
| 39 | 6.55 |
| 50 | 7.72 |
（血球体积，ｍｍ），
（红血球数，百万）
(1) 画出上表的散点图;
(2)求出回归直线并且画出图形；
(3)若血球体积为49ｍｍ，预测红血球数大约是多少？