题目内容

抛物线y²=2px上弦长为a（a≥2p）的弦的中点到y轴的距离的最小值为：________．

$\text{[math]}$
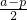
分析：根据题意可求得抛物线的准线方程和焦点坐标，记弦的两端点为A、B，AB的中点为M，它们在l上的射影分别是A₁，B₁，M₁；利用抛物线的定义可求得|AF|=|AA₁|，|BF|=|BB₁|，进而表示出M到y轴的距离d，分析出当A，B，F共线时等号成立求得答案．
解答：抛物线的准线l的方程为：x=- $\text{[math]}$ ，焦点F（ $\text{[math]}$ ，0），
记弦的两端点为A、B，AB的中点为M，它们在l上的射影分别是A₁，B₁，M₁；
于是有：|AF|=|AA₁|，|BF|=|BB₁|，
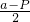M到y轴的距离d=|MM₁|- $\text{[math]}$ = $\text{[math]}$ （|AA₁|+|BB₁|）- $\text{[math]}$ = $\text{[math]}$ （|AF|+|BF|）- $\text{[math]}$ ≥ $\text{[math]}$ |AB|- $\text{[math]}$ = $\text{[math]}$ ，当且仅当A，B，F共线时等号成立．
点评：本题主要考查了抛物线的简单性质．过焦点的弦最短是通径，长为2p．

练习册系列答案

寒假作业内蒙古人民出版社系列答案

寒假作业人民教育出版社系列答案

寒假作业云南人民出版社系列答案

寒假作业宁夏人民教育出版社系列答案

寒假作业时代出版传媒股份有限公司系列答案

寒假作业华中科技大学出版社系列答案

复习计划100分寒假学期复习系列答案

寒假作业江西高校出版社系列答案

寒假作业欢乐共享快乐假期系列答案

寒假作业及活动系列答案

相关题目

下列命题正确的是（　　）
①动点M至两定点A、B的距离之比为常数λ（λ＞0且λ≠1）．则动点M的轨迹是圆．
②椭圆

=1(a＞b＞0)的离心率e=

，则b=c(c为半焦距）．
③双曲线

=1(a＞0，b＞0)的焦点到渐近线的距离为b．
④已知抛物线y²=2px上两点A（x₁，y₁），B（x₂，y₂）且OA⊥OB（O为原点），则y₁y₂=-p²．

A、②③④	B、①④
C、①②③	D、①③

抛物线的方程是y²=2x，有一个半径为1的圆，圆心在x轴上运动问这个圆运动到什么位置时，圆与抛物线在交点处的切线互相垂直？（注：设P（x₀，y₀）是抛物线y²=2px上一点，则抛物线在P点处的切线斜率是

给出下列四个命题：
①如果椭圆

=1的一条弦被点A（4，2）平分，那么这条弦所在的直线的斜率为-

；
②过点P（0，1）与抛物线y²=x有且只有一个交点的直线共有3条．
③双曲线

=1(a＞0，b＞0)的焦点到渐近线的距离为b．
④已知抛物线y²=2px上两点A（x₁，x₂），B（x₂，y₂）且OA⊥OB（O为原点），则y₁y₂=-p²．
其中正确的命题有

（请写出你认为正确的命题的序号）

抛物线y²=2px上一点M（4，m）到准线的距离为6，则p=

抛物线y²=2px上一点Q（6，y₀），且知Q点到焦点的距离为10，则焦点到准线的距离是（　　）