题目内容
已知M(a,b),N(sinωx,cosωx)(ω>0),记f(x)=
•
(O为坐标原点).若f(x)的最小正周期为2,并且当x=
时,f(x)的最大值为5.
(1)求函数f(x)的表达式;
(2)对任意的整数n,在区间(n,n+1)内是否存在曲线y=f(x)的对称轴?若存在,求出此对称轴方程;若不存在,说明理由.
| OM |
| ON |
| 1 |
| 3 |
(1)求函数f(x)的表达式;
(2)对任意的整数n,在区间(n,n+1)内是否存在曲线y=f(x)的对称轴?若存在,求出此对称轴方程;若不存在,说明理由.
(1)由题设条件知f(x)=asinωx+bcosωx=5sin(ωx+φ),
由已知得
,得ω=π,φ=
,
所以f(x)=5sin(πx+
),.
(2)曲线f(x) 有对称轴x=x0的充要条件是5sin(πx0+
)=±5.即πx0+
=kπ+
即x0=k+
,k∈Z,
令n<k+
<n+1 得k=n (n∈Z),
所以在区间(n,n+1)内存在曲线f(x)的对称轴,
其方程是x=n+
,n∈Z,
由已知得
|
| π |
| 6 |
所以f(x)=5sin(πx+
| π |
| 6 |
(2)曲线f(x) 有对称轴x=x0的充要条件是5sin(πx0+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 3 |
令n<k+
| 1 |
| 3 |
所以在区间(n,n+1)内存在曲线f(x)的对称轴,
其方程是x=n+
| 1 |
| 3 |

练习册系列答案
相关题目
 (O为坐标原点).若f(x)的最小正周期为2,并且当x=
(O为坐标原点).若f(x)的最小正周期为2,并且当x= 时,f(x)的最大值为5.
时,f(x)的最大值为5.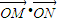 (O为坐标原点).若f(x)的最小正周期为2,并且当x=
(O为坐标原点).若f(x)的最小正周期为2,并且当x= 时,f(x)的最大值为5.
时,f(x)的最大值为5.