题目内容
已知M(a,b),N(sinωx,cosωx)(ω>0),记f(x)=| OM |
| ON |
| 1 |
| 3 |
(1)求函数f(x)的表达式;
(2)对任意的整数n,在区间(n,n+1)内是否存在曲线y=f(x)的对称轴?若存在,求出此对称轴方程;若不存在,说明理由.
分析:(1)先由内积公式求出函数f(x)的表达式再逆用和差角公式化简,据周期为2与函数过点(
,5)求参数.
(2)解出对称轴的方程,看其形式是不是可以表示成一个整数加上一个大于零且小于1的数.若是则存在,若否,则不存在.求解发现,本题结论是存在.
| 1 |
| 3 |
(2)解出对称轴的方程,看其形式是不是可以表示成一个整数加上一个大于零且小于1的数.若是则存在,若否,则不存在.求解发现,本题结论是存在.
解答:解:(1)由题设条件知f(x)=asinωx+bcosωx=5sin(ωx+φ),
由已知得
,得ω=π,φ=
,
所以f(x)=5sin(πx+
),.
(2)曲线f(x) 有对称轴x=x0的充要条件是5sin(πx0+
)=±5.即πx0+
=kπ+
即x0=k+
,k∈Z,
令n<k+
<n+1 得k=n (n∈Z),
所以在区间(n,n+1)内存在曲线f(x)的对称轴,
其方程是x=n+
,n∈Z,
由已知得
|
| π |
| 6 |
所以f(x)=5sin(πx+
| π |
| 6 |
(2)曲线f(x) 有对称轴x=x0的充要条件是5sin(πx0+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 3 |
令n<k+
| 1 |
| 3 |
所以在区间(n,n+1)内存在曲线f(x)的对称轴,
其方程是x=n+
| 1 |
| 3 |
点评:本题考查用向量的数量积公式变形得到函数的表达式,然后再利用和差角公式变形,根据题目条件求出参数得到函数的表达式,本题综合性较强.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 (O为坐标原点).若f(x)的最小正周期为2,并且当x=
(O为坐标原点).若f(x)的最小正周期为2,并且当x= 时,f(x)的最大值为5.
时,f(x)的最大值为5.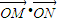 (O为坐标原点).若f(x)的最小正周期为2,并且当x=
(O为坐标原点).若f(x)的最小正周期为2,并且当x= 时,f(x)的最大值为5.
时,f(x)的最大值为5.