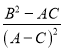题目内容
【题目】对于双曲线![]() ,若点P(x0,y0)满足
,若点P(x0,y0)满足![]() ,则称P在
,则称P在![]() 的外部,若点P(x0,y0)满足
的外部,若点P(x0,y0)满足![]() >1,则称
>1,则称![]() 在的内部;
在的内部;
(1)若直线y=kx+1上的点都在C(1,1)的外部,求k的取值范围;
(2)若C(a,b)过点(2,1),圆x2+y2=r2(r>0)在C(a,b)内部及C(a,b)上的点构成的圆弧长等于该圆周长的一半,求b、r满足的关系式及r的取值范围;
(3)若曲线|xy|=mx2+1(m>0)上的点都在C(a,b)的外部,求m的取值范围.
【答案】(1)k>![]() 或k<﹣
或k<﹣![]() (2)
(2)![]() ,
,![]() (3)
(3)![]()
【解析】
(1)由题意可得直线上点P(x0,y0)满足![]()
![]() ,且
,且![]() ,即为
,即为![]() 恒成立,运用二次项系数小于0和判别式小于0,解不等式即可得到所求范围;
恒成立,运用二次项系数小于0和判别式小于0,解不等式即可得到所求范围;
(2)将(2,1)代入双曲线的方程,由圆和双曲线的相交的弦长相等,弦所对的圆周角均为90°,且均为![]() ,联立圆的方程和双曲线的方程,求得交点坐标,可得弦长,化简整理可得b、r的关系式和r的范围;
,联立圆的方程和双曲线的方程,求得交点坐标,可得弦长,化简整理可得b、r的关系式和r的范围;
(3))|xy|=mx2+1(m>0),即为![]() ,由题意可得曲线上点P(x0,y0)满足
,由题意可得曲线上点P(x0,y0)满足![]() ,代入
,代入![]() ,整理成
,整理成![]() 的二次不等式,运用换元法和二次函数的性质,解不等式即可得到所求范围.
的二次不等式,运用换元法和二次函数的性质,解不等式即可得到所求范围.
解:(1)直线y=kx+1上的点都在C(1,1)的外部,可得
直线上点P(x0,y0)满足![]()
![]() ,且
,且![]() ,
,
即为![]() ,恒成立,
,恒成立,
可得![]() ,且
,且![]() ,
,
即有![]() ,解得
,解得![]() 或
或![]() ;
;
(2)若C(a,b)过点(2,1),可得![]() ,
,
即为![]() ,
,
由圆和双曲线的相交的弦长相等,
弦所对的圆周角均为90°,且均为![]() ,
,
联立 ,解得
,解得![]() ,
,
可得![]() ,
,
化简可得 ,
,
令![]() ,则
,则![]() ,
,
即有![]() ;
;
(3)|xy|=mx2+1(m>0),即为![]() ,
,
由曲线|xy|=mx2+1(m>0)上的点都在C(a,b)的外部,
可得曲线上点P(x0,y0)满足![]() ,
,
即为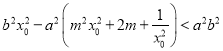 ,
,
即有![]() ,
,
令![]() ,即有
,即有![]() ,对
,对![]() 恒成立,
恒成立,![]() 时,
时,![]() 显然成立;
显然成立;![]() 时,
时,![]() 且
且 ,
,
由![]() ,可得
,可得![]() ,
,
解得![]() .
.

练习册系列答案
相关题目