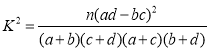题目内容
【题目】设函数![]() 的图象在
的图象在![]() 处取得极值4.
处取得极值4.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对于函数![]() ,若存在两个不等正数
,若存在两个不等正数![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,则把区间
,则把区间![]() 叫函数
叫函数![]() 的“正保值区间”.问函数
的“正保值区间”.问函数![]() 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
【答案】(1)![]() 的递增区间是
的递增区间是![]() 和
和![]() ,递减区间是
,递减区间是![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】
(1)由极值求出参数![]() ,由导数的正负确定单调区间;
,由导数的正负确定单调区间;
(2)根据函数的单调性分类讨论,首先确定两个极值点不能在![]() 上,再按函数在
上,再按函数在![]() 上的单调性求解.
上的单调性求解.
(1)![]() ,
,
依题意则有:![]() ,即
,即![]() 解得
解得![]() ,
,
∴![]() .令
.令![]() ,
,
由![]() 解得
解得![]() 或
或![]() ,
,
所以函数![]() 的递增区间是
的递增区间是![]() 和
和![]() ,递减区间是
,递减区间是![]() ;
;
(2)设函数![]() 的“正保值区间”是
的“正保值区间”是![]() ,因为
,因为![]() ,故极值点
,故极值点![]() 不在区间
不在区间![]() 上;
上;
①若极值点![]() 在区间
在区间![]() ,此时
,此时![]() ,在此区间上
,在此区间上![]() 的最大值是
的最大值是![]() 4,不可能等于
4,不可能等于![]() ;故在区间
;故在区间![]() 上没有极值点;
上没有极值点;
②若![]() 在
在![]() 上单调递增,即
上单调递增,即![]() 或
或![]() ,
,
则![]() ,即
,即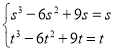 ,解得
,解得![]() 或
或![]() 不符合要求;
不符合要求;
③若![]() 在
在![]() 上单调减,即
上单调减,即![]() ,则
,则![]() ,
,
两式相减并除![]() 得:
得:![]() , ①
, ①
两式相除可得![]() ,即
,即![]() ,
,
整理并除以![]() 得:
得:![]() ,②
,②
由①、②可得![]() ,即s,t是方程
,即s,t是方程![]() 的两根,
的两根,
解得![]() ,
,![]() ,但
,但![]() 不合要求.
不合要求.
综上可得不存在满足条件的s、t,即函数![]() 不存在“正保值区间”
不存在“正保值区间”

【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生的选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计选考科目人数如下表:
名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从选考方案确定的![]() 名学生中随机选出
名学生中随机选出![]() 名,试求在选取的
名,试求在选取的![]() 名学生中恰有
名学生中恰有![]() 名男生的条件下两名学生的选考方案中都含有历史学科的概率;
名男生的条件下两名学生的选考方案中都含有历史学科的概率;
(3)从选考方案确定的![]() 名男生中随机选出
名男生中随机选出![]() 名,设随机变量
名,设随机变量![]() 表示所选
表示所选![]() 人中选考方案完全相同的人数(若有
人中选考方案完全相同的人数(若有![]() 组
组![]() 人选考方案完全相同,则
人选考方案完全相同,则![]() ),求
),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.