Question

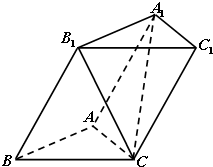如图，三棱柱ABC-A₁B₁C₁的各棱长均为2，侧面BCC₁B₁⊥底面ABC，侧棱BB₁与底面ABC所成的角为60°．
（Ⅰ）求直线A₁C与底面ABC所成的角；
（Ⅱ）在线段A₁C₁上是否存在点P，使得平面B₁CP⊥平面ACC₁A₁？若存在，求出C₁P的长；若不存在，请说明理由．

Answer 1

（本题满分14分）
解：（Ⅰ）过B₁作B₁O⊥BC于O，
∵侧面BCC₁B₁⊥平面ABC，
∴B₁O⊥平面ABC，
∴∠B₁BC=60°．
又∵BCC₁B₁是菱形，∴O为BC的中点．…（2分）
以O为坐标原点，如图建立空间直角坐标系，
则，B（0，-1，0），C（0，1，0），，，
∴，又底面ABC的法向量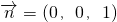…（4分）
设直线A₁C与底面ABC所成的角为θ，
则，∴θ=45°
所以，直线A₁C与底面ABC所成的角为45°． …（7分）
（Ⅱ）假设在线段A₁C₁上存在点P，设=，
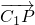则，，
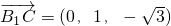．…（8分）
设平面B₁CP的法向量，
则．
令z=1，则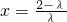，，∴． …（10分）
设平面ACC₁A₁的法向量，
则
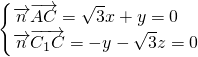
令z=1，则，x=1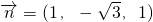，∴． …（12分）
要使平面B₁CP⊥平面ACC₁A₁，
则==．
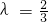∴．∴． …（14分）
分析：（Ⅰ）过B₁作B₁O⊥BC于O，证明B₁O⊥平面ABC，以O为坐标原点，如图建立空间直角坐标系，求出A，B，C，A₁，B₁，C₁坐标，底面ABC的法向量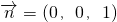，设直线A₁C与底面ABC所成的角为θ，通过，求出直线A₁C与底面ABC所成的角．
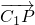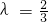（Ⅱ）假设在线段A₁C₁上存在点P，设=，通过求出平面B₁CP的法向量，利用求出平面ACC₁A₁的法向量，通过=0，求出．．求解．
点评：本题考查直线与平面垂直，直线与平面所成的角，平面与平面垂直，考查空间想象能力，计算能力．