题目内容
（本小题满分12分）如图，已知正方体ABCD—A1B1C1D1的棱长为2，E、F分别是A1B1、CC1的中点，过D1、E、F作平面D1EGF交BB1于G。 （1）求证：EG//D1F； （2）求锐二面角C1—D1E—F的余弦值。
(Ⅰ) 见解析 (Ⅱ) 
解析:
（1）证明：在正方体ABCD—A1B1C1D1中，
平面ABB1A1//平面DCC1D1??。
平面
平面ABB1A1=EG，
平面平面DCC1D1=D1F，
4分
（2）解：如图，以D为原点分别以DA、DC、DD1为
轴、
轴、z轴，建立空间直角坐标系，
则有
6分
设平面D1EGF的法向量为
则由
，
得
取
，所以
8分
又平面C1D1E的法向为
9分
所以，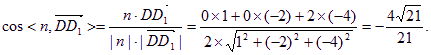
所以，锐二面角C1—D1E—F的余弦值为 12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
