题目内容
下列命题中,真命题的个数有( )
①函数y=2-x是单调递减函数;
②x0是方程lnx+x=4的解,则x0∈(2,3);
③?x∈R,x2-x+
≥0;
④?a,b∈R,则“3a>3b”是“log3a>log3b”的充要条件.
①函数y=2-x是单调递减函数;
②x0是方程lnx+x=4的解,则x0∈(2,3);
③?x∈R,x2-x+
| 1 |
| 4 |
④?a,b∈R,则“3a>3b”是“log3a>log3b”的充要条件.
分析:①函数y=2-x是单调递减函数;②x0是方程lnx+x=4的解,令f(x)=lnx+x-4,则f(1)=-3<0,f(2)=ln2-2<0,f(3)=ln3-1>0,f(4)=ln4>0.所以f(2)与f(3)异号.所以x0∈(2,3);③由x2-x+
=(x-
)2≥0,知?x∈R,x2-x+
≥0;④当a≤0,b≤0时,log3a和log3b不存在.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:①函数y=2-x是单调递减函数,故①是真命题;
②x0是方程lnx+x=4的解,令f(x)=lnx+x-4,
则f(1)=-3<0,f(2)=ln2-2<0,f(3)=ln3-1>0,f(4)=ln4>0.
所以f(2)与f(3)异号.所以x0∈(2,3),故②正确;
③∵x2-x+
=(x-
)2≥0,∴?x∈R,x2-x+
≥0,故③成立;
④当a≤0,b≤0时,log3a和log3b不存在,故④不成立.
故选C.
②x0是方程lnx+x=4的解,令f(x)=lnx+x-4,
则f(1)=-3<0,f(2)=ln2-2<0,f(3)=ln3-1>0,f(4)=ln4>0.
所以f(2)与f(3)异号.所以x0∈(2,3),故②正确;
③∵x2-x+
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
④当a≤0,b≤0时,log3a和log3b不存在,故④不成立.
故选C.
点评:本题考查命题的真假判断及其应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
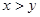 ,则
,则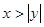 ”的逆命题
”的逆命题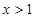 ,则
,则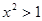 ”的否命题
”的否命题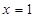 ,则
,则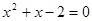 ”的否命题
”的否命题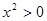 ,则
,则