题目内容
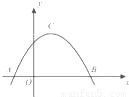
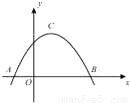
 如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是
如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是| 3π |
| 4 |
| 3π |
| 4 |
分析:由图象可知:C点的纵坐标即为函数f(x)的最大值,|AB|即为函数f(x)的周期的一半,即可得出答案.
解答:解:∵函数f(x)=3sin(2x-φ),
∴函数f(x)的最大值为3,即点C的纵坐标;
又∵T=
=π,∴|AB|=
T=
.
∴S△=
×3×
=
.
故答案为
.
∴函数f(x)的最大值为3,即点C的纵坐标;
又∵T=
| 2π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
∴S△=
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
故答案为
| 3π |
| 4 |
点评:掌握三角函数的图象和性质是解题的关键.

练习册系列答案
相关题目
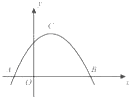 如图,A,B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则
如图,A,B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则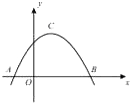 如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是________.
如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是________.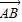 •
•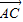 的值为 .
的值为 .