题目内容
已知函数
 .
.
(Ⅰ)若 在
在 处的切线垂直于直线
处的切线垂直于直线 ,求该点的切线方程,并求此时函数
,求该点的切线方程,并求此时函数 的单调区间;
的单调区间;
(Ⅱ)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ) 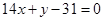 ,
, 的单调递增区间是
的单调递增区间是 ;单调递减区间是
;单调递减区间是 和
和 ;
;
(Ⅱ) 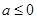 或
或 .
.
解析试题分析:(Ⅰ)通过切线垂直直线可以得到切线的斜率,解出 ,将
,将 代入求出切点坐标,从而求出切线方程,令
代入求出切点坐标,从而求出切线方程,令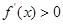 和
和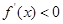 分别求出函数的单调递增区间和递减区间;(Ⅱ)通过对
分别求出函数的单调递增区间和递减区间;(Ⅱ)通过对 的讨论,求出
的讨论,求出 在
在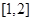 上的最大值,令
上的最大值,令 ,解出
,解出 的取值范围.
的取值范围.
试题解析:(Ⅰ)  ,根据题意
,根据题意 ,解得
,解得 ,
,
此时切点坐标是 ,故所求的切线方程是
,故所求的切线方程是 ,即
,即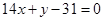 .
.
当 时,
时,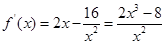 ,
,
令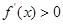 ,解得
,解得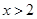 ,令
,令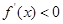 ,解得
,解得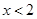 且
且 ,故函数
,故函数 的单调递增区间是
的单调递增区间是 ;单调递减区间是
;单调递减区间是 和
和 . 5分
. 5分
(Ⅱ) 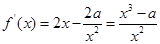 .
.
①若 ,则
,则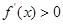 在区间
在区间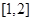 上恒成立,
上恒成立, 在区间
在区间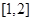 上单调递增,函数
上单调递增,函数 在区间
在区间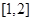 上的最大值为
上的最大值为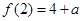 ; 7分
; 7分
②若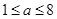 ,则在区间
,则在区间 上
上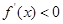 ,函数单调递减,在区间
,函数单调递减,在区间 上
上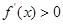 ,函数单调递增,故函数
,函数单调递增,故函数 在区间
在区间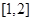 上的最大值为
上的最大值为 ,
,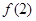 中的较大者,
中的较大者, ,故当
,故当 时,函数的最大值为
时,函数的最大值为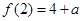 ,当
,当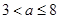 时,函数的最大值为
时,函数的最大值为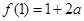 ; 9分
; 9分
③当 时,
时,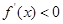 在区间
在区间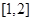 上恒成立,函数
上恒成立,函数 在区间
在区间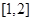 上单调递减,函数的最大值为
上单调递减,函数的最大值为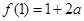 . 11分
. 11分
综上可知,在区间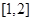 上,当
上,当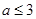 时,函数
时,函数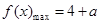 ,当
,当 时,函数
时,函数 .
.
不等式 对任意的
对任意的 恒成立等价于在区间
恒成立等价于在区间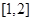 上,
上, ,故当
,故当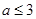 时,
时,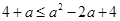 ,即
,即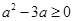 ,解得
,解得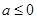 或
或 ;当
;当 时,
时, ,即
,即

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
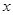 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量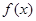 (万件)近似满足:
(万件)近似满足: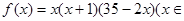 N*,且
N*,且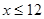 )
)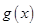 (万件)与月份
(万件)与月份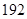 万件;
万件; 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应,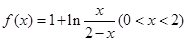 .
.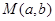 ,使得函数
,使得函数 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数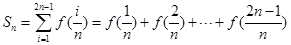 ,其中
,其中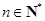 ,求
,求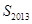 ;
;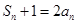 ,若不等式
,若不等式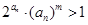 对
对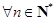 且
且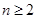 恒成立,求实数
恒成立,求实数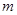 的取值范围.
的取值范围. 在
在 处取得极值。
处取得极值。 ;
;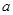 ,使得对任意
,使得对任意 ?若存在,求
?若存在,求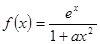 ,其中
,其中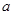 为正实数,
为正实数,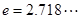 .
.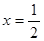 是
是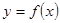 的一个极值点,求
的一个极值点,求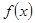 的单调区间.
的单调区间. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时,函数
时,函数 图象上的点都在
图象上的点都在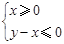 所表示的平面区域内,求实数
所表示的平面区域内,求实数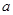 的取值范围.
的取值范围. ,点
,点 为一定点,直线
为一定点,直线 分别与函数
分别与函数 的图象和
的图象和 轴交于点
轴交于点 ,
, ,记
,记 的面积为
的面积为 .
. 时,求函数
时,求函数 时, 若
时, 若 ,使得
,使得 , 求实数
, 求实数 的取值范围.
的取值范围. .
.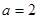 时,对任意
时,对任意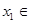 R,存在
R,存在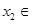 R,使
R,使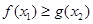 ,求实数
,求实数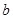 的取值范围;
的取值范围;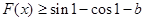 对任意
对任意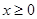 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.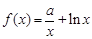 ,
,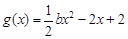 ,
,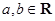
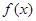 的单调区间;
的单调区间;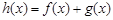 ,当
,当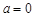 时,
时,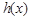 在
在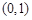 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数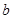 的取值范围;
的取值范围;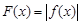 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线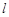 与
与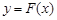 的图象有两个切点
的图象有两个切点