题目内容

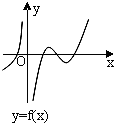设函数y=f（x）的图象如图所示，则导函数y=f′（x）可能为（　　）
分析：利用函数的单调性和导数之间的关系，确定导数值的符号．
解答：解：由函数f（x）的图象可知，当x＜0时，函数单调递增，此时f′（x）＞0，排除A，C．
当x＞0时，函数先单调递增，然后单调递减，最后单调递增，所以导数的符号为先为正，后卫负，最后为正数．
所以对应的图象为D．
故选D．
点评：本题主要考查函数的图象的识别和判断，利用函数单调性和导数之间的关系是解决本题的关键．原函数看函数的单调性，导函数看函数的符号．
练习册系列答案
相关题目
设函数y=f（x）的定义域为R，并且满足f（x+y）=f（x）+f（y），f(
13
)=1，且当x＞0时，f（x）＞0．
（1）求f（0）的值；
（2）判断函数的奇偶性；
（3）如果f（x）+f（2+x）＜2，求x取值范围．
设函数y=f（x）的定义域为全体R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）成立，数列{an}满足a1=f（0），且f(an+1)=
1
f(
-an
2an+1
)
（n∈N*）
（Ⅰ）求证：y=f（x）是R上的减函数；          
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）若不等式
k
(1+a1)(1+a2)…(1+an)
-
1
2n+1
≤0对一切n∈N*均成立，求k的最大值．
设函数y=f（x）的定义域为R+，若对于给定的正数k，定义函数：fk(x)=
k，f(x)≤k
f(x)，f(x)＞k
，则当函数f(x)=
1
x
，k=1时，函数fk（x）的图象与直线x=
1
4
，x=2，y=0围成的图形的面积为（　　）
（2007•闵行区一模）（文）设函数y=f（x）的反函数是y=f-1（x），且函数y=f（x）过点P（2，-1），则f-1（-1）=
2
2
．
（2008•南汇区二模）设函数y=f（x）的定义域为R，对任意实数x，y都有f（x+y）=f（x）+f（y），当x＞0时f（x）＜0且f（3）=-4．
（1）求证：y=f（x）为奇函数；
（2）在区间[-9，9]上，求y=f（x）的最值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网