题目内容
如图所示,椭圆C: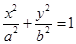
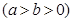 的一个焦点为F(1,0),且过点(2,0)
的一个焦点为F(1,0),且过点(2,0)
(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点,且直线AB垂直于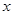 轴,又直线
轴,又直线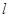 :
: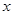 =4与
=4与 轴交于点N,直线AF与BN交
轴交于点N,直线AF与BN交
于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

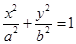
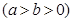 的一个焦点为F(1,0),且过点(2,0)
的一个焦点为F(1,0),且过点(2,0)(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点,且直线AB垂直于
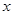 轴,又直线
轴,又直线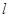 :
: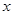 =4与
=4与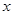 轴交于点N,直线AF与BN交
轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

解:(1)由题设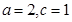 ,从而
,从而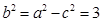 ,
,
所以椭圆C的方程为+=1.………………………3分
(2)(i)证明:由题意得F(1,0)、N(4,0).
设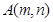 ,则
,则 ,
, .①
.①
AF与BN的方程分别为: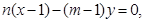
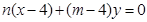 .
.
设 ,则有
,则有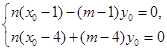
由上得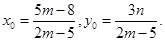
由于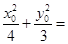
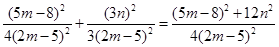
=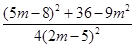 =1.
=1.
所以点M恒在椭圆C上.………………………………7分
(ⅱ)解:设AM的方程为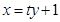 ,代入
,代入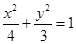 ,
,
得
设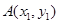 、
、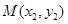 ,则有
,则有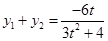 ,
, .
.
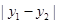 =
=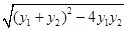 =
=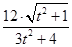 .
.
令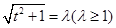 ,则
,则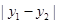 =
=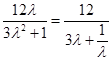
因为函数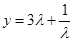 在
在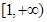 为增函数,
为增函数,
所以当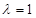 即
即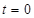 时,函数
时,函数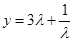 有最小值4.
有最小值4.
即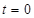 时,
时,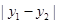 有最大值3,此时AM过点F.……11分
有最大值3,此时AM过点F.……11分
△AMN的面积S△AMN=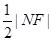 ·
·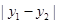 有最大值
有最大值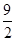 .…………12分
.…………12分
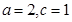 ,从而
,从而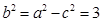 ,
, 所以椭圆C的方程为+=1.………………………3分
(2)(i)证明:由题意得F(1,0)、N(4,0).
设
 ,则
,则 ,
, .①
.①AF与BN的方程分别为:
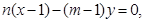
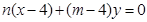 .
. 设
 ,则有
,则有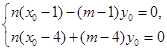
由上得
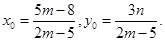
由于
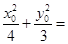
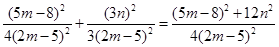
=
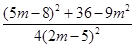 =1.
=1.所以点M恒在椭圆C上.………………………………7分
(ⅱ)解:设AM的方程为
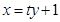 ,代入
,代入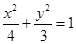 ,
,得

设
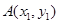 、
、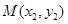 ,则有
,则有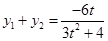 ,
, .
.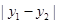 =
=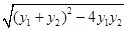 =
=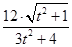 .
.令
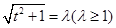 ,则
,则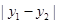 =
=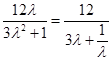
因为函数
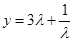 在
在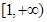 为增函数,
为增函数,所以当
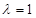 即
即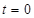 时,函数
时,函数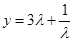 有最小值4.
有最小值4.即
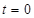 时,
时,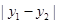 有最大值3,此时AM过点F.……11分
有最大值3,此时AM过点F.……11分△AMN的面积S△AMN=
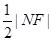 ·
·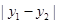 有最大值
有最大值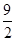 .…………12分
.…………12分略

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 :
: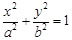 (
(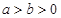 )的离心率为
)的离心率为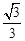 ,直线
,直线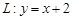 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 ,右焦点为
,右焦点为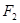 ,直线
,直线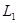 过点
过点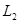 垂直
垂直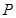 ,线段
,线段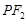 的垂直平分线交
的垂直平分线交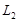 于点
于点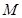 .
.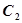 的方程;
的方程;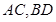 为点
为点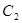 的过点
的过点 面积的最小值.
面积的最小值.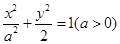 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,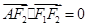 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为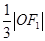 .
.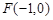 ,交 y轴于点M,若
,交 y轴于点M,若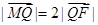 ,求直线l 的斜率.
,求直线l 的斜率.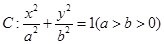 恒过定点
恒过定点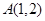 ,则椭圆的中心到准线的距离的
,则椭圆的中心到准线的距离的 +
+ =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.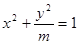 的下焦点为
的下焦点为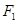 、上焦点为
、上焦点为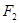 ,其离心 率
,其离心 率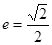 。过焦点F2且与
。过焦点F2且与 轴不垂直的直线l交椭圆于A、B两点。
轴不垂直的直线l交椭圆于A、B两点。 的值;
的值;  是椭圆
是椭圆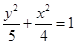 上的一点,
上的一点,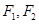 是焦点,且
是焦点,且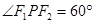 ,则
,则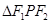 的面积为
的面积为 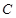 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在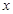 轴上,椭圆上的点到
轴上,椭圆上的点到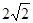 ,离心率
,离心率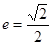 .
.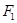 、
、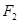 ,过点
,过点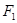 的直线
的直线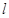 与该椭圆交于点
与该椭圆交于点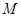 、
、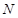 ,
, 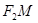 、
、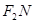 为邻边作平行四边形
为邻边作平行四边形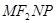 ,求该平行四边形对角线
,求该平行四边形对角线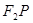 的长度
的长度  的离心率为( )
的离心率为( )


