题目内容
已知向量 ,函数
,函数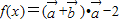 .
.(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)已知a、b、c分别为△ABC内角A、B、C的对边,其中A为锐角,
 ,且f(A)=1,求A,b和△ABC的面积S.
,且f(A)=1,求A,b和△ABC的面积S.
【答案】分析:(I)利用向量数量积的坐标表示可得,结合辅助角公式可得,f(x)=sin(2x-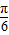 ),利用周期公式
),利用周期公式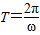 可求
可求
(II)由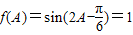 结合
结合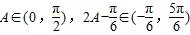 可得
可得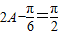 ,
,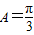 ,由余弦定理可得,a2=b2+c2-2bccosA,从而有
,由余弦定理可得,a2=b2+c2-2bccosA,从而有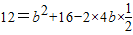 ,即b2-4b+4=0,解方程可得b,代入三角形面积公式可求.
,即b2-4b+4=0,解方程可得b,代入三角形面积公式可求.
解答:(本小题满分12分)
解:(Ⅰ)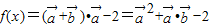 =
= (2分)
(2分)
= =
= =
=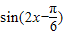 (4分)
(4分)
因为ω=2,所以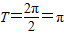 (6分)
(6分)
(Ⅱ)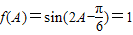
因为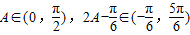 ,所以
,所以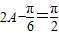 ,
, (8分)
(8分)
则a2=b2+c2-2bccosA,所以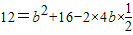 ,即b2-4b+4=0
,即b2-4b+4=0
则b=2(10分)
从而 (12分)
(12分)
点评:本题主要考查了向量的数量积的坐标表示,辅助角公式的应用,三角函数的周期公式的应用,由三角函数值求角,及三角形的面积公式.综合的知识比较多,但试题的难度不大,
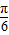 ),利用周期公式
),利用周期公式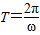 可求
可求(II)由
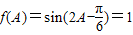 结合
结合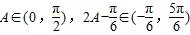 可得
可得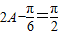 ,
,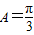 ,由余弦定理可得,a2=b2+c2-2bccosA,从而有
,由余弦定理可得,a2=b2+c2-2bccosA,从而有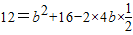 ,即b2-4b+4=0,解方程可得b,代入三角形面积公式可求.
,即b2-4b+4=0,解方程可得b,代入三角形面积公式可求.解答:(本小题满分12分)
解:(Ⅰ)
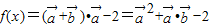 =
= (2分)
(2分)=
 =
= =
=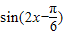 (4分)
(4分)因为ω=2,所以
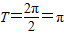 (6分)
(6分)(Ⅱ)
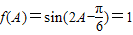
因为
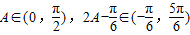 ,所以
,所以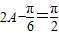 ,
, (8分)
(8分)则a2=b2+c2-2bccosA,所以
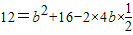 ,即b2-4b+4=0
,即b2-4b+4=0则b=2(10分)
从而
 (12分)
(12分)点评:本题主要考查了向量的数量积的坐标表示,辅助角公式的应用,三角函数的周期公式的应用,由三角函数值求角,及三角形的面积公式.综合的知识比较多,但试题的难度不大,

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
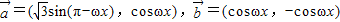 ,函数
,函数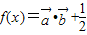 (ω>0)的图象的两相邻对称轴间的距离为
(ω>0)的图象的两相邻对称轴间的距离为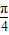 .
.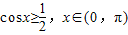 ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值. ,函数
,函数 的最大值为6,最小正周期为π.
的最大值为6,最小正周期为π. 个单位,再向上平移1个单位,得到函数y=g(x)的图象.求
个单位,再向上平移1个单位,得到函数y=g(x)的图象.求 上的值域.
上的值域. ,函数
,函数 的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点
的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点 .
. ,函数
,函数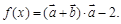 (Ⅰ)求函数
(Ⅰ)求函数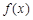 的最小正周期
的最小正周期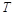 ;(Ⅱ)将函数
;(Ⅱ)将函数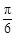 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数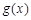 的图像,求函数
的图像,求函数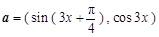 ,函数
,函数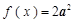 .求:
.求: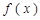 的最小值;
的最小值;