题目内容
已知向量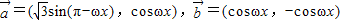 ,函数
,函数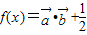 (ω>0)的图象的两相邻对称轴间的距离为
(ω>0)的图象的两相邻对称轴间的距离为 .
.(1)求ω值;
(2)若
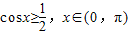 ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值.
【答案】分析:符号错误:w应该是ω.
(1)利用两个向量的数量积的运算求出f(x)=sin(2ωx-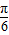 ),再根据图象的两相邻对称轴间的距离为
),再根据图象的两相邻对称轴间的距离为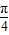 求得ω=2.
求得ω=2.
(2)若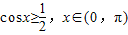 ,求得-
,求得- ≤sin(4x-
≤sin(4x- )≤1,令t=4x-
)≤1,令t=4x-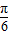 ,h(t)=sint,t∈(-
,h(t)=sint,t∈(-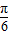 ,
,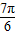 ],则函数 h(t)的图象和直线y=m只有一个交点,数形结合求出m的值
],则函数 h(t)的图象和直线y=m只有一个交点,数形结合求出m的值
解答: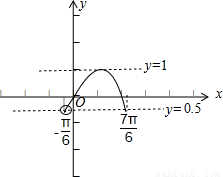 解:(1)函数
解:(1)函数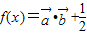 =
=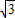 sin(π-ωx)cosωx-cos2ωx+
sin(π-ωx)cosωx-cos2ωx+ =
= sin2ωx-
sin2ωx- +
+ =sin(2ωx-
=sin(2ωx-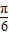 ),
),
再由函数f(x)的图象的两相邻对称轴间的距离为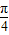 可得
可得 •
•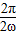 =
=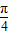 ,解得ω=2,函数f(x)=sin(4x-
,解得ω=2,函数f(x)=sin(4x-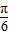 ).
).
(2)若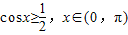 ,则有 0<x≤
,则有 0<x≤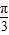 ,-
,-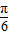 <4x-
<4x-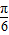 ≤
≤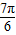 ,-
,- ≤sin(4x-
≤sin(4x- )≤1.
)≤1.
由f(x)=m有且仅有一个实根,可得函数f(x) 的图象和直线y=m只有一个交点.
令t=4x- ,h(t)=sint,t∈(-
,h(t)=sint,t∈(-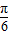 ,
,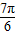 ],则函数 h(t)的图象和直线y=m只有一个交点,如图所示:
],则函数 h(t)的图象和直线y=m只有一个交点,如图所示:
数形结合可得∴m=1,或m=- .
.
点评:本题主要考查两个向量的数量积的运算,函数y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,体现了数形结合的数学思想,属于中档题.
(1)利用两个向量的数量积的运算求出f(x)=sin(2ωx-
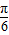 ),再根据图象的两相邻对称轴间的距离为
),再根据图象的两相邻对称轴间的距离为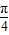 求得ω=2.
求得ω=2.(2)若
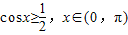 ,求得-
,求得- ≤sin(4x-
≤sin(4x- )≤1,令t=4x-
)≤1,令t=4x-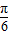 ,h(t)=sint,t∈(-
,h(t)=sint,t∈(-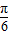 ,
,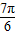 ],则函数 h(t)的图象和直线y=m只有一个交点,数形结合求出m的值
],则函数 h(t)的图象和直线y=m只有一个交点,数形结合求出m的值解答:
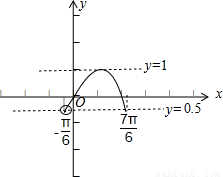 解:(1)函数
解:(1)函数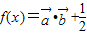 =
=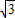 sin(π-ωx)cosωx-cos2ωx+
sin(π-ωx)cosωx-cos2ωx+ =
= sin2ωx-
sin2ωx- +
+ =sin(2ωx-
=sin(2ωx-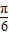 ),
),再由函数f(x)的图象的两相邻对称轴间的距离为
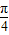 可得
可得 •
•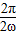 =
=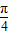 ,解得ω=2,函数f(x)=sin(4x-
,解得ω=2,函数f(x)=sin(4x-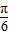 ).
).(2)若
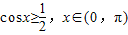 ,则有 0<x≤
,则有 0<x≤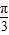 ,-
,-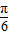 <4x-
<4x-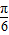 ≤
≤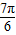 ,-
,- ≤sin(4x-
≤sin(4x- )≤1.
)≤1.由f(x)=m有且仅有一个实根,可得函数f(x) 的图象和直线y=m只有一个交点.
令t=4x-
 ,h(t)=sint,t∈(-
,h(t)=sint,t∈(-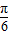 ,
,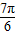 ],则函数 h(t)的图象和直线y=m只有一个交点,如图所示:
],则函数 h(t)的图象和直线y=m只有一个交点,如图所示:数形结合可得∴m=1,或m=-
 .
.点评:本题主要考查两个向量的数量积的运算,函数y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
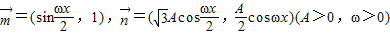 ,函数
,函数 的最大值为6,最小正周期为π.
的最大值为6,最小正周期为π.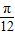 个单位,再向上平移1个单位,得到函数y=g(x)的图象.求
个单位,再向上平移1个单位,得到函数y=g(x)的图象.求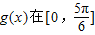 上的值域.
上的值域.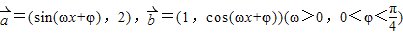 ,函数
,函数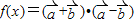 的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点
的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点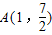 .
.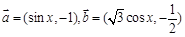 ,函数
,函数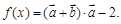 (Ⅰ)求函数
(Ⅰ)求函数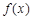 的最小正周期
的最小正周期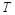 ;(Ⅱ)将函数
;(Ⅱ)将函数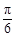 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数 的图像,求函数
的图像,求函数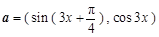 ,函数
,函数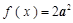 .求:
.求: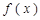 的最小值;
的最小值;