题目内容
已知曲线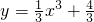 ,则过点P(2,4)的切线方程是
,则过点P(2,4)的切线方程是
- A.4x-y-4=0或y=x+2
- B.4x-y+4=0
- C.x-4y+14=0
- D.2x-y=0
A
分析:根据导数的几何意义求出函数在x=2处的导数,从而求得切线的斜率,再用点斜式写出化简即可.
解答:设切点(x,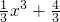 )
)
∵P(2,4)在y= x3+
x3+ 上,又y′=x2,
上,又y′=x2,
∴斜率 .解得x=-1,x=2,
.解得x=-1,x=2,
x=2时切点就是P点,解出的切线方程为4x-y-4=0
x=-1时,解出的切线方程为y=x+2
故选A
点评:本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于基础题.
分析:根据导数的几何意义求出函数在x=2处的导数,从而求得切线的斜率,再用点斜式写出化简即可.
解答:设切点(x,
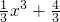 )
)∵P(2,4)在y=
 x3+
x3+ 上,又y′=x2,
上,又y′=x2,∴斜率
 .解得x=-1,x=2,
.解得x=-1,x=2,x=2时切点就是P点,解出的切线方程为4x-y-4=0
x=-1时,解出的切线方程为y=x+2
故选A
点评:本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
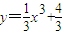 ,则过点P(2,4)的切线方程为 .
,则过点P(2,4)的切线方程为 .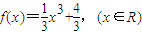 ,则过点P(2,f(2))的切线方程为( )
,则过点P(2,f(2))的切线方程为( )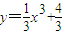 ,则过点P(2,4)的切线方程是( )
,则过点P(2,4)的切线方程是( )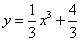 ,则过点P(2,4)的切线方程是( )。
,则过点P(2,4)的切线方程是( )。