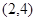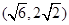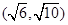题目内容
已知直线y=mx与函数 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.(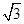 ,4) ,4) |
B.( ,+∞) ,+∞) |
C.( ,5) ,5) |
D.(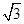 , , ) ) |
B
解析作出函数 的图象,如图所示.
的图象,如图所示.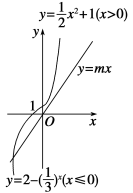
直线y=mx的图象是绕坐标原点旋转的动直线.当斜率m≤0时,直线y=mx与函数f(x)的图象只有一个公共点;当m>0时,直线y=mx始终与函数y=2-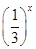 (x≤0)的图象有一个公共点,故要使直线y=
(x≤0)的图象有一个公共点,故要使直线y=
mx与函数f(x)的图象有三个公共点,必须使直线y=mx与函数y=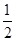 x2+1 (x>0)的图象有两个公共点,即方程mx=
x2+1 (x>0)的图象有两个公共点,即方程mx=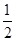 x2+1在x>0时有两个不相等的实数根,即方程x2-2mx+2=0的判别式Δ=4m2-4×2>0,解得m>
x2+1在x>0时有两个不相等的实数根,即方程x2-2mx+2=0的判别式Δ=4m2-4×2>0,解得m> .故所求实数m的取值范围是(
.故所求实数m的取值范围是( ,+∞).
,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
将函数 的图象向左平移
的图象向左平移 个单位长度后得到函数
个单位长度后得到函数 ,则函数
,则函数 ( )
( )
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数,也不是偶函数 |
函数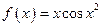 在区间[0,4]上的零点个数为( )
在区间[0,4]上的零点个数为( )
| A.4 | B.5 | C.6 | D.7 |
函数f(x)=2x2-lnx的单调递增区间是( )
A. |
B.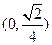 |
C.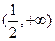 |
D.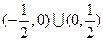 |
设函数g(x)=x2-2(x∈R),f(x)=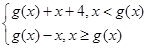 则f(x)的值域是( )
则f(x)的值域是( )
A.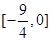 ∪(1,+∞) ∪(1,+∞) |
| B.[0,+∞) |
C.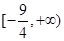 |
D.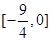 ∪(2,+∞) ∪(2,+∞) |
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+ ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )
| A.[1,2] |
B. |
C. |
| D.(0,2] |
函数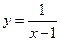 的图像与函数
的图像与函数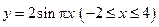 的图像所有交点的横坐标之和等于( )
的图像所有交点的横坐标之和等于( )
| A.2 |
| B.4 |
| C.6 |
| D.8 |
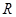 上的偶函数
上的偶函数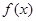 满足
满足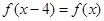 ,且在区间[0,2]上
,且在区间[0,2]上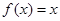 ,若关于
,若关于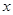 的方程
的方程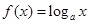 有三个不同的根,则
有三个不同的根,则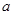 的范围为( )
的范围为( )