题目内容
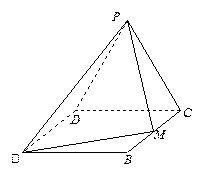
如右图所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为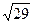 ,设这条最短路线与CC1的交点为N.求:
,设这条最短路线与CC1的交点为N.求:
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.
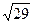 ,设这条最短路线与CC1的交点为N.求:
,设这条最短路线与CC1的交点为N.求:
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.
(1)其对角线长为
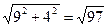 .
.
(2) PC=P1C=2,
NC=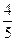 .
.
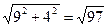 .
.(2) PC=P1C=2,
NC=
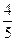 .
.(1)正三棱柱ABC—A1B1C1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为
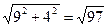 .
.
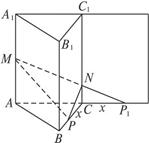
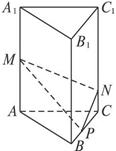
(2)如右图所示,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连结MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.
设PC=x,则P1C=x.
在Rt△MAP1中,
由勾股定理得(3+x)2+22=29,
求得x=2.∴PC=P1C=2,
∵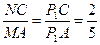 ,∴NC=
,∴NC=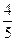 .
.
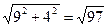 .
.
(2)如右图所示,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连结MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.
设PC=x,则P1C=x.
在Rt△MAP1中,
由勾股定理得(3+x)2+22=29,
求得x=2.∴PC=P1C=2,
∵
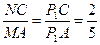 ,∴NC=
,∴NC=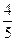 .
.
练习册系列答案
相关题目
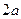 ,DC=
,DC= , F是BE的中点。
, F是BE的中点。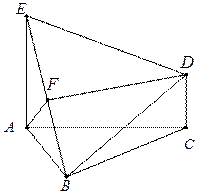
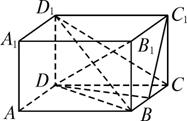
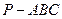 中,
中,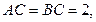 ∠
∠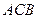 =90°,
=90°,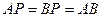 ,
,
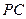 ⊥
⊥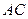 .
. (Ⅰ)求证:
(Ⅰ)求证: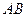 ;
; 的体积.
的体积.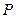 为正方形
为正方形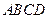 所在平面外一点,且
所在平面外一点,且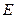 为
为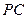 中点.求证:(1)
中点.求证:(1)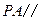 面
面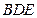 ; (2)面
; (2)面 面
面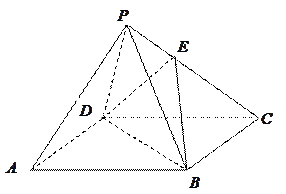
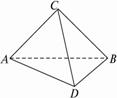
 的等边△
的等边△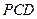 所在的平面垂直于矩形
所在的平面垂直于矩形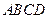 所在的平面,
所在的平面,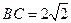 ,
,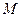 为
为 的中点.
的中点.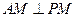 ;
;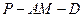 的大小.
的大小.