题目内容
(本小题满分12分)
已知定义在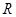 上的函数
上的函数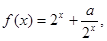
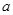 为常数,若
为常数,若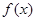 为偶函数,
为偶函数,
(1)求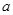 的值;
的值;
(2)判断函数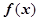 在
在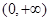 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;
(3)求函数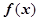 的值域.
的值域.
(1) ;(2)定义法证明
;(2)定义法证明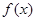 在
在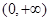 上单调增;(3)函数的值域为
上单调增;(3)函数的值域为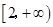 。
。
解析试题分析:(1)由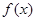 为偶函数,
为偶函数,
得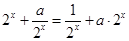 ,
,
从而 ;
; 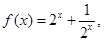
(2)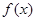 在
在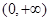 上单调增
上单调增
证明:任取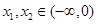 且
且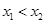 ,
, 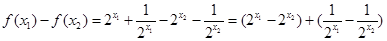
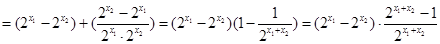 ,
,
当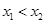 ,且
,且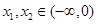 ,
,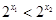 ,
,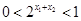
从而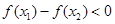 ,即
,即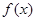 在
在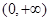 上单调增;
上单调增;
(3)函数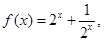
令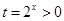 ,则
,则 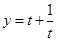
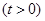
函数在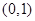 递减,在
递减,在 递增.(这里要简要的证明一下,假如没有证明扣1分)..14分
递增.(这里要简要的证明一下,假如没有证明扣1分)..14分
所以函数的值域为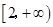 …
…
考点:本题主要考查函数的奇偶性、单调性,指数幂的运算。
点评:典型题,研究函数的奇偶性、单调性,是高一阶段研究的主要函数性质,往往以具体函数为载体,综合考查学生灵活运用知识的能力。本题中(3)小题得到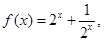 后,利用换元思想,转化成“对号函数”的研究,值得注意。
后,利用换元思想,转化成“对号函数”的研究,值得注意。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
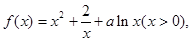
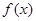 在
在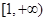 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 对于区间
对于区间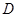 上的任意两个值
上的任意两个值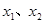 总有以下不等式
总有以下不等式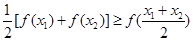 成立,则称函数
成立,则称函数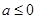 时,
时,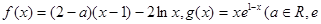 为自然对数的底数).
为自然对数的底数).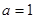 时,求
时,求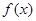 的单调区间;若函数
的单调区间;若函数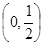 上无零点,求
上无零点,求 最小值;
最小值;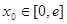 ,在
,在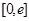 上总存在两个不同的
上总存在两个不同的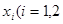 ),使
),使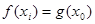 成立,求
成立,求
 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围; ,若
,若 的图象与
的图象与 上有两个交点,求
上有两个交点,求 的取值范围。
的取值范围。
 时,求
时,求 的单调区间;
的单调区间; ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 上是单调函数
上是单调函数 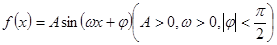 在一个周期内的部分函数图象如图所示,(I)求函数
在一个周期内的部分函数图象如图所示,(I)求函数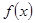 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数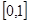 上的最大值和最小值.
上的最大值和最小值.
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
. 解集.
解集. 。
。 ,求a的值;
,求a的值; 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m) 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。