题目内容
若f(sinx)=3-cos2x,则f(cosx)=( )
| A.3-cos2x | B.3-sin2x | C.3+cos2x | D.3+sin2x |
C
提示:方法一:由于f(sinx)=3-cos2x=2sin2x+2,得到f(x)=2x2+2,
则f(cosx)=2cos2 x +2=3+cos2x;方法二:f(cosx)= f(sin(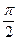 -x))=3-cos2(
-x))=3-cos2(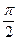 -x)=3-cos(
-x)=3-cos(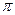 -2x)=3+cos2x.
-2x)=3+cos2x.
则f(cosx)=2cos2 x +2=3+cos2x;方法二:f(cosx)= f(sin(
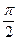 -x))=3-cos2(
-x))=3-cos2(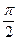 -x)=3-cos(
-x)=3-cos(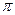 -2x)=3+cos2x.
-2x)=3+cos2x.

练习册系列答案
相关题目
 .
.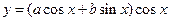 有最大值
有最大值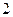 ,最小值
,最小值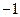 ,则实数
,则实数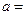 ____,
____,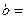 ___。
___。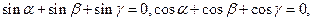 求
求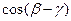 的值.
的值.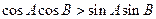 ,则△ABC为( )
,则△ABC为( )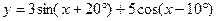 的最大值是 .
的最大值是 .
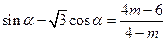 有意义,则应有( )
有意义,则应有( )