题目内容
已知acosα+bsinα=c, acosβ+bsinβ=c(ab≠0,α–β≠kπ, k∈Z)求证: .
.
 .
.证明略
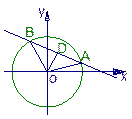
在平面直角坐标系中,点A(cosα,sinα)与点B(cosβ,
sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点如图.
从而: |AB|2=(cosα–cosβ)2+(sinα–sinβ)2
=2–2cos(α–β)
又∵单位圆的圆心到直线l的距离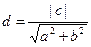
由平面几何知识知|OA|2–(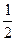 |AB|)2=d2即
|AB|)2=d2即
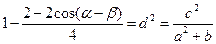
∴

sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点如图.
从而: |AB|2=(cosα–cosβ)2+(sinα–sinβ)2
=2–2cos(α–β)

又∵单位圆的圆心到直线l的距离
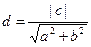
由平面几何知识知|OA|2–(
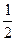 |AB|)2=d2即
|AB|)2=d2即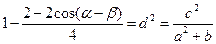
∴



练习册系列答案
相关题目
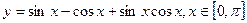 的最大值和最小值。
的最大值和最小值。 。
。 的值;
的值; 的值。
的值。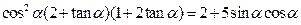 。
。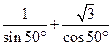 ;
;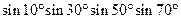 .
.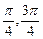 ),β∈(0,
),β∈(0,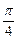 ),cos(α-
),cos(α-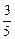 ,sin(
,sin(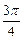 +β)=
+β)=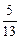 ,则sin(α+β)=_________.
,则sin(α+β)=_________. 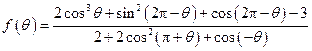 ,求
,求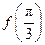 的值.
的值. =( )
=( ) B、
B、 C、1 D、
C、1 D、