题目内容
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:
①FG⊥BD
②B1D⊥面EFG
③面EFG∥面ACC1A1
④EF∥面CDD1C1
正确结论的序号是( )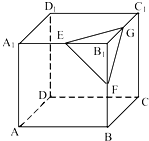
A.①和②
B.②和④
C.①和③
D.③和④
【答案】B
【解析】解:如图连接A1C1、A1B、BC1、BD、B1D,因为E、F、G分别是棱A1B1、BB1、B1C1的中点
①因为FG∥BC1 , △BDC1是正三角形,所以∠C1BD=60°,因为FG∥BC1 , 所以异面直线FG与BD所成的角为60°,
FG⊥BD不正确,所以①不正确.
②因为平面A1C1B∥平面EFG,并且B1D⊥平面A1C1B,所以B1D⊥面EFG,所以②正确.
③因为EF和FG和平面面ACC1A1不平行,所以③错误.
④EF∥平面CDD1C1内的D1C,所以EF∥面CDD1C1 . 所以④正确.
故选B.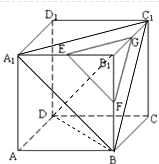
【考点精析】本题主要考查了命题的真假判断与应用和空间中直线与平面之间的位置关系的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点才能正确解答此题.

练习册系列答案
相关题目
