题目内容
【题目】把五个标号为1到5的小球全部放入标号为1到4的四个盒子中,并且不许有空盒,那么任意一个小球都不能放入标有相同标号的盒子中的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意可以分两类,第一类第5球独占一盒,第二类,第5球不独占一盒,根据分类计数原理得到答案.
解:第一类,第5球独占一盒,则有4种选择;
如第5球独占第一盒,则剩下的三盒,先把第1球放旁边,就是2,3,4球放入2,3,4盒的错位排列,有2种选择,
再把第1球分别放入2,3,4盒,有3种可能选择,于是此时有![]() 种选择;
种选择;
如第1球独占一盒,有3种选择,剩下的2,3,4球放入两盒有2种选择,此时有![]() 种选择,
种选择,
得到第5球独占一盒的选择有![]() 种,
种,
第二类,第5球不独占一盒,先放![]() 号球,4个球的全不对应排列数是9;第二步放5号球:有4种选择;
号球,4个球的全不对应排列数是9;第二步放5号球:有4种选择;![]() ,
,
根据分类计数原理得,不同的方法有![]() 种.
种.
而将五球放到4盒共有![]() 种不同的办法,
种不同的办法,
故任意一个小球都不能放入标有相同标号的盒子中的概率![]()
故选:![]() .
.

练习册系列答案
相关题目
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取![]() 件产品作为样本称出它们的质量(单位:毫克),质量值落在
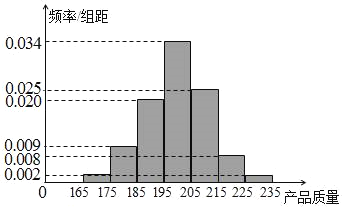
件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)以样本的频率作为概率,试估计从甲流水线上任取![]() 件产品,求其中不合格品的件数
件产品,求其中不合格品的件数![]() 的数学期望.
的数学期望.
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅱ)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
(Ⅲ)由乙流水线的频率分布直方图可以认为乙流水线生产的产品质量![]() 服从正态分布
服从正态分布![]() ,求质量
,求质量![]() 落在
落在![]() 上的概率.
上的概率.
参考公式:![]()
![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
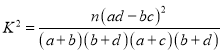 ,其中
,其中![]() .
.