题目内容
过椭圆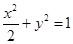 的左焦点
的左焦点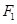 作直线
作直线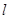 交椭圆于
交椭圆于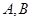 两点,
两点,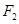 是椭圆右焦点,则
是椭圆右焦点,则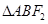 的周长为( )
的周长为( )
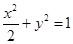 的左焦点
的左焦点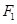 作直线
作直线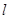 交椭圆于
交椭圆于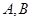 两点,
两点,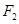 是椭圆右焦点,则
是椭圆右焦点,则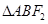 的周长为( )
的周长为( )A. | B.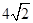 | C. | D. |
B
试题分析:由椭圆的定义知:
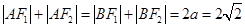 ,∴
,∴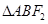 的周长为
的周长为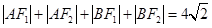 ,故选B
,故选B点评:熟练掌握椭圆的定义是解决此类问题的关键,属基础题

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
题目内容
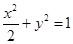 的左焦点
的左焦点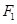 作直线
作直线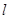 交椭圆于
交椭圆于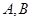 两点,
两点,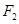 是椭圆右焦点,则
是椭圆右焦点,则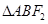 的周长为( )
的周长为( )A. | B.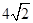 | C. | D. |
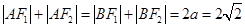 ,∴
,∴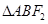 的周长为
的周长为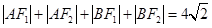 ,故选B
,故选B
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案