题目内容
17. 如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )
如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
分析 判断四面体A′BDA为正四面体,取BD的中点E,连接AE,A′E,由等腰三角形“三线合一”的性质,易得∠AEA′即为侧面与底面所成二面角的平面角,解三角形AA′E即可得到正四面体侧面与底面所成二面角的余弦值.
解答 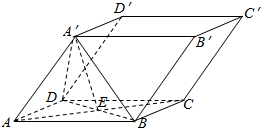 解:棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则四面体A′BDA为正四面体.
解:棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则四面体A′BDA为正四面体.
取BD的中点E,连接AE,A′E,设四面体的棱长为2,则AE=A′E=$\sqrt{3}$
且AE⊥BD,A′E⊥BD,则∠AEA′即为侧面与底面所成二面角的平面角,
在△AA′E中,cos∠AEA′=$\frac{{AE}^{2}+{A′E}^{2}-{A′A}^{2}}{2AE•A′E}$=$\frac{1}{3}$
故正四面体侧面与底面所成二面角的余弦值是:$\frac{1}{3}$.
故选:A.
点评 本题考查的知识点是二面角的平面角及求法,其中确定∠AEA′即为相邻两侧面所成二面角的平面角,是解答本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
2.已知集合 A={x|x2-x-12>0},B={x|x≥m}.若 A∩B={x|x>4},则实数m的取值范围是(( )
| A. | (-4,3) | B. | [-3,4] | C. | (-3,4) | D. | (-∞,4] |