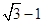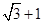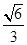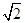题目内容
(本小题满分14分)
在△ABC中,角A、B、C所对的边分别是a、b、c,且(a+b+c)(b+c-a)=3bc.
(1)求角A的度数;
(2)若2b=3c,求tanC的值.
在△ABC中,角A、B、C所对的边分别是a、b、c,且(a+b+c)(b+c-a)=3bc.
(1)求角A的度数;
(2)若2b=3c,求tanC的值.
(1)A=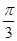 (2)tanC=
(2)tanC=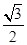 .
.
(注:第(2)问也可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,再计算出sinC的值,从而得到tanC的值.可以仿照此标准进行给分.)
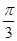 (2)tanC=
(2)tanC=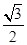 .
. (注:第(2)问也可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,再计算出sinC的值,从而得到tanC的值.可以仿照此标准进行给分.)
本试题主要是考查了运用正弦定理和余弦定理来求解三角形的综合运用。
(1)首先将给定的关系式(a+b+c)(b+c-a)=3bc,利用余弦定理变形,得到关于A角的余弦公式,从而得到结论。
(2)可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,从而得到结论。
解: (1)由(a+b+c)(b+c-a)=3bc得(b+c)2-a2=bc,所以cosA=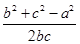 =
=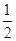 ,
,
又Ax∈(0,p),所以A=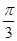 . ············ 6分
. ············ 6分
(2)由正弦定理得,2b=3c⇒2sinB=3sinC ············ 8分
⇒2sin(A+C)=3sinC⇒2sin(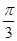 +C)=3sinC
+C)=3sinC
⇒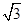 cosC+ sinC =3sinC ··········· 11分
cosC+ sinC =3sinC ··········· 11分
⇒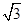 cosC=2sinC⇒tanC=
cosC=2sinC⇒tanC=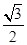 . ··········· 14分
. ··········· 14分
(注:第(2)问也可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,再计算出sinC的值,从而得到tanC的值.可以仿照此标准进行给分.)
(1)首先将给定的关系式(a+b+c)(b+c-a)=3bc,利用余弦定理变形,得到关于A角的余弦公式,从而得到结论。
(2)可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,从而得到结论。
解: (1)由(a+b+c)(b+c-a)=3bc得(b+c)2-a2=bc,所以cosA=
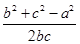 =
=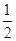 ,
,又Ax∈(0,p),所以A=
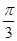 . ············ 6分
. ············ 6分(2)由正弦定理得,2b=3c⇒2sinB=3sinC ············ 8分
⇒2sin(A+C)=3sinC⇒2sin(
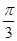 +C)=3sinC
+C)=3sinC⇒
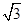 cosC+ sinC =3sinC ··········· 11分
cosC+ sinC =3sinC ··········· 11分⇒
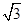 cosC=2sinC⇒tanC=
cosC=2sinC⇒tanC=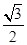 . ··········· 14分
. ··········· 14分(注:第(2)问也可以通过所给的边2b=3c的关系,代入已知条件,用一条边表示另外两条边,再用余弦定理计算出cosC的值,再计算出sinC的值,从而得到tanC的值.可以仿照此标准进行给分.)

练习册系列答案
相关题目
 =(2b-c,a),
=(2b-c,a), =(cosA,-cosC),且
=(cosA,-cosC),且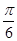 )取最大值时,求角
)取最大值时,求角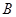 的大小.
的大小.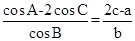 .
.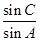 的值;
的值;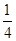 ,△
,△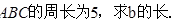
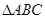 中,
中,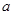 ,
,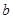 ,
,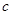 分别为内角
分别为内角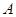 ,
,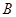 ,
,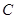 所对的边,且满足
所对的边,且满足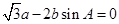 .
.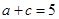 ,且
,且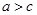 ,
,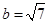 ,求
,求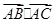 的值.
的值. 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、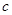 ,已知
,已知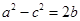 ,且
,且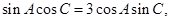 则b=____________.
则b=____________.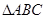 中,
中,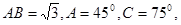 则
则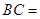 ( )
( )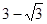
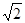
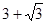
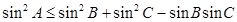 ,则A的取值范围是( )
,则A的取值范围是( ) 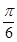 ]
]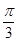 ]
]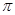 )
) 中,
中, ,
, ,面积
,面积 ,则
,则





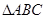 中,已知
中,已知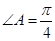 ,
,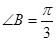 ,
,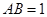 ,则
,则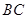 为
为