题目内容
动点P（x，y）到点F（0，1）的距离与它到直线y+1=0的距离相等，则动点P的轨迹方程为 ．
【答案】分析：由抛物线的定义，可得点P位于以F为焦点、直线y=-1为准线的抛物线上．因此设P的轨迹方程为x2=2px（p＞0），根据抛物线的简单几何性质即可求出点P的轨迹方程．
解答：解：∵直线l：y+1=0即y=-1，而点P（x，y）到点F（0，1）的距离等于P到直线l的距离
∴点P位于以F为焦点、直线l：y=-1为准线的抛物线上，
因此，设P的轨迹方程为x2=2px，（p＞0）
可得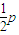
=1，解得p=2，2p=4
∴动点P的轨迹方程为x2=4y．
故答案为：x2=4y
点评：本题给出动点满足的条件，求该点的轨迹方程，着重考查了圆锥曲线的定义和轨迹方程的求法等知识，属于基础题．
解答：解：∵直线l：y+1=0即y=-1，而点P（x，y）到点F（0，1）的距离等于P到直线l的距离
∴点P位于以F为焦点、直线l：y=-1为准线的抛物线上，
因此，设P的轨迹方程为x2=2px，（p＞0）
可得
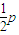=1，解得p=2，2p=4∴动点P的轨迹方程为x2=4y．
故答案为：x2=4y
点评：本题给出动点满足的条件，求该点的轨迹方程，着重考查了圆锥曲线的定义和轨迹方程的求法等知识，属于基础题．
练习册系列答案
相关题目