题目内容
甲、乙两公司生产同一种新产品,经测算,对于任意x≥0,存在两个函数f(x),g(x)。当甲公司投入 x万元用于产品的宣传时,若乙公司投入的宣传费用小于f(x)万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入x万元用于产品的宣传时,若甲公司投入的宣传费用小于g(x)万元,则甲公司有失败的风险,否则无失败风险。
(1)请分别解释f(0)=17与g(0)=19的实际意义;
(2)当 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用?
(1)请分别解释f(0)=17与g(0)=19的实际意义;
(2)当
 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用? 解:(1)f(0)=17的实际意义是当甲公司不进行产品的宣传时,乙公司为了保证无失败的风险,至少要投入17万元用于产品宣传;
g(0)=19的实际意义是当乙公司不进行产品的宣传时,甲公司为了保证无失败的风险,至少要投入19万元用于产品宣传。
(2)设甲公司投入宣传费用m万元,乙公司投入宣传费用n万元,
则当且仅当 时,双方均无失败风险
时,双方均无失败风险
∴
∴
即甲、乙两公司分别应投入24万元和25万元进行产品宣传。
g(0)=19的实际意义是当乙公司不进行产品的宣传时,甲公司为了保证无失败的风险,至少要投入19万元用于产品宣传。
(2)设甲公司投入宣传费用m万元,乙公司投入宣传费用n万元,
则当且仅当
 时,双方均无失败风险
时,双方均无失败风险 ∴

∴

即甲、乙两公司分别应投入24万元和25万元进行产品宣传。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 、
、 及任意的
及任意的 ,当甲公司投放
,当甲公司投放 万元改造设备时,若乙公司投放改造设备费用小于
万元改造设备时,若乙公司投放改造设备费用小于 、
、 的实际意义;
的实际意义; ,
, ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?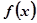 、
、 及任意的
及任意的 ,当甲公司投入
,当甲公司投入 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于 的实际意义;
的实际意义;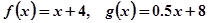 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用? 、
、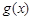 及任意的
及任意的 ,当甲公司投放
,当甲公司投放 万元改造设备时,若乙公司投放改造设备费用小于
万元改造设备时,若乙公司投放改造设备费用小于 、
、 的实际意义;
的实际意义; ,
, ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?