题目内容
设函数f(x)=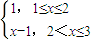 ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).(I)求函数h(a)的解析式;
(II)画出函数y=h(x)的图象并指出y=h(x)的最小值.
【答案】分析:(I) 先化简g(x)的解析式,当a<0时,当a>1时,当0≤a≤1时,分别求出最大值与最小值的差为h(a).
(II )画出y=h(x)的图象,数形结合,求出 y=h(x)的最小值.
解答: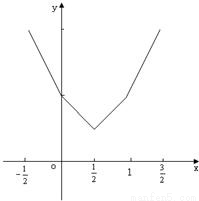 解:(I) g(x)=
解:(I) g(x)=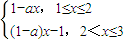 ,
,
(1)当a<0时,函数g(x)是[1,3]增函数,此时,
g(x)max=g(3)=2-3a,
g(x)min=g(1)=1-a,所以h(a)=1-2a.
(2)当a>1时,函数g(x)是[1,3]减函数,此时,
g(x)min=g(3)=2-3a,
g(x)max=g(1)=1-a,所以h(a)=2a-1.
(3)当0≤a≤1时,若x∈[1,2],则g(x)=1-ax,有
g(2)≤g(x)≤g(1);
若x∈[2,3],则g(x)=(1-a)x-1,有g(2)≤g(x)≤g(3);
因此,g(x)min=g(2)=1-2a,
而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤ 时,g(x)max=g(3)=2-3a,有h(a)=1-a.
时,g(x)max=g(3)=2-3a,有h(a)=1-a.
当 <a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
<a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
综上所述:h(a)=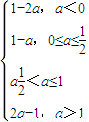 .
.
(II)画出y=h(x)的图象,如图:数形结合,可得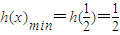 .
.
点评:本题考查求函数的最大值、最小值的方法,体现了数形结合、及分类讨论的数学思想.
(II )画出y=h(x)的图象,数形结合,求出 y=h(x)的最小值.
解答:
 解:(I) g(x)=
解:(I) g(x)=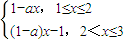 ,
,(1)当a<0时,函数g(x)是[1,3]增函数,此时,
g(x)max=g(3)=2-3a,
g(x)min=g(1)=1-a,所以h(a)=1-2a.
(2)当a>1时,函数g(x)是[1,3]减函数,此时,
g(x)min=g(3)=2-3a,
g(x)max=g(1)=1-a,所以h(a)=2a-1.
(3)当0≤a≤1时,若x∈[1,2],则g(x)=1-ax,有
g(2)≤g(x)≤g(1);
若x∈[2,3],则g(x)=(1-a)x-1,有g(2)≤g(x)≤g(3);
因此,g(x)min=g(2)=1-2a,
而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤
 时,g(x)max=g(3)=2-3a,有h(a)=1-a.
时,g(x)max=g(3)=2-3a,有h(a)=1-a.当
 <a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
<a≤1时,g(x)max=g(1)=1-a,有h(a)=a.综上所述:h(a)=
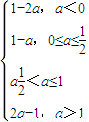 .
.(II)画出y=h(x)的图象,如图:数形结合,可得
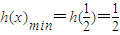 .
.点评:本题考查求函数的最大值、最小值的方法,体现了数形结合、及分类讨论的数学思想.

练习册系列答案
相关题目