题目内容
( )圆 关于直线
关于直线 对称的圆的方程是
对称的圆的方程是
A. | B. |
C. | D. |
D.
解析试题分析:设圆心(-1,0)关于直线2x-y-3=0的对称点为(a,b),
则 ,解之得
,解之得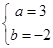 ,
,
所以对称圆的圆心为(3,-2),半径不变,所以所求圆的方程为 .
.
考点:点关于直线的对称,圆的标准方程.
点评:圆关于直线的对称,实质是圆心关于直线的对称,根据点关于直线对称的求法,求出对称圆的圆心坐标,半径不变.

练习册系列答案
相关题目
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x-1)2+(y-1)2=4 |
| C.(x+3)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
圆 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )
A. | B. |
C. | D. |
已知直角坐标系中圆 方程为
方程为 ,
, 为圆内一点(非圆心),
为圆内一点(非圆心),
那么方程 所表示的曲线是———————— ( )
所表示的曲线是———————— ( )
A.圆 |
B.比圆 半径小,与圆 半径小,与圆 同心的圆 同心的圆 |
C.比圆 半径大与圆 半径大与圆 同心的圆 同心的圆 |
| D.不一定存在 |
直线 相切,则实数
相切,则实数 等于( )
等于( )
A. | B. | C. | D. |
过原点且倾斜角为 的直线被圆学
的直线被圆学 所截得的弦长为
所截得的弦长为
A. | B.2 | C. | D.2 |
由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
| A.1 | B. | C.2 | D.3 |
方程 表示圆,则
表示圆,则 的取值范围是
的取值范围是
A. 或 或 | B. |
C. | D. 或 或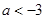 |
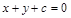 上,则点(m,c)不满足下列哪个方程( )
上,则点(m,c)不满足下列哪个方程( )


