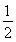题目内容
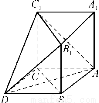
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,G、H分别为DC、BC的中点.
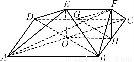
(1)求证:平面FGH∥平面BDE;
(2)求证:平面ACF⊥平面BDE.
(1)见解析(2)见解析
【解析】学生错【解析】
证明:
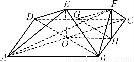
(1)如图,设AC与BD交于点O,连结OE、OH.由已知EF=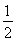 AB,得EF∥
AB,得EF∥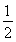 AB.
AB.
∵OH∥=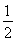 AB,∴EF∥=OH,∴四边形OEFH为平行四边形,∴FH∥EO.
AB,∴EF∥=OH,∴四边形OEFH为平行四边形,∴FH∥EO.
∵G、H分别为DC、BC的中点,∴GH∥DB.∴平面FGH∥平面BDE.
(2)由四边形ABCD为正方形,有AB⊥BC.又EF∥AB,∴EF⊥BC,
而EF⊥FB,∴EF⊥平面BFC.∵FH 平面BFC,∴EF⊥FH.
平面BFC,∴EF⊥FH.
∴AB⊥FH.又BF=FC,H为BC的中点,∴FH⊥BC,∴FH⊥平面ABCD.
∴FH⊥AC.又FH∥EO,∴AC⊥EO.又AC⊥BD,∴AC⊥平面BDE.
又AC 平面ACF,∴平面ACF⊥平面BDE.
平面ACF,∴平面ACF⊥平面BDE.
审题引导:(1)探索求解过程的关键是弄清线线平行?线面平行?面面平行;线线垂直?线面垂直?面面垂直;不要跳步造成错误,如本例(1),易出现由线线平行直接推得面面平行,从而导致证明过程错误.(2)正确理解运用线线、线面、面面的平行、垂直关系的判定定理和性质定理,特别注意将条件写完整,不可遗漏,如本例(2)在证明线、面垂直时,没有指出线线相交,就直接写出线面垂直,造成导致证明过程不严谨.
规范解答:证明:(1)设AC与BD交于点O,连结OE、OH,由已知EF= AB,得EF∥
AB,得EF∥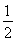 AB.(2分)
AB.(2分)
∵OH∥=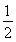 AB,∴EF∥=OH,∴四边形OEFH为平行四边形,∴FH∥EO.(4分)
AB,∴EF∥=OH,∴四边形OEFH为平行四边形,∴FH∥EO.(4分)
∵FH?平面BDE,EO?平面BDE,∴FH∥平面BDE.
∵G、H分别为DC、BC的中点,∴GH∥DB.
∵GH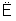 平面BDE,DB
平面BDE,DB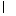 平面BDE,∴GH∥平面BDE.又∵FH∩GH=H,
平面BDE,∴GH∥平面BDE.又∵FH∩GH=H,
∴平面FGH∥平面BDE.(6分)
(2)由四边形ABCD为正方形,有AB⊥BC.又EF∥AB,∴EF⊥BC,(8分)
而EF⊥FB,BC∩FB=B,∴EF⊥平面BFC.FH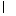 平面BFC,∴EF⊥FH.(10分)
平面BFC,∴EF⊥FH.(10分)
∴AB⊥FH,又BF=FC,H为BC的中点,∴FH⊥BC,AB∩BC=B,∴FH⊥平面ABCD.
∴FH⊥AC,又FH∥EO,∴AC⊥EO.(12分)又AC⊥BD,EO∩BD=O,∴AC⊥平面BDE.
又AC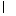 平面ACF,∴平面ACF⊥平面BDE.(14分)
平面ACF,∴平面ACF⊥平面BDE.(14分)
错因分析:证明两平面平行、垂直关系时一定要正确运用两平面平行或垂直的判定定理,并将相应的条件写全.本题(1)直接由线线平行推得面面平行,不符合面面平行的判定定理,导致证明过程不严谨.(2)在证明线、面垂直时,没有指出相交的条件;导致证题过程不正确.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案