题目内容
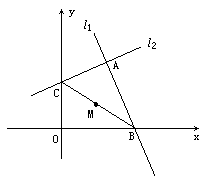
过定点A(a,b)(a≠0)任作两条互相垂直的直线l1、l2,且l1、l2分别与x轴、y轴交于M、N点,求线段MN的中点P的轨迹方程.
答案:
解析:
解析:
|
设点P的坐标为(x,y),则点M,N的坐标分别为(2x,0),(0,2y) 当x≠ 因为AM⊥AN,所以kAM·kAN=-1,即 当x= 所以所求方程为2ax+2by-a2-b2=0. |

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 时,kAM=
时,kAM= ,kAN=
,kAN= .
. =-1,化简得2ax+2by-a2-b2=0.
=-1,化简得2ax+2by-a2-b2=0. 时,AM⊥x轴,点P(
时,AM⊥x轴,点P( ,
, )也适合上一方程.
)也适合上一方程. ,分别与x轴,y轴相交于B,C两点,求线段BC的中点M的轨迹方程.
,分别与x轴,y轴相交于B,C两点,求线段BC的中点M的轨迹方程.