题目内容
已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足![]() ,
,![]() .
.
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上.
答案:
解析:
解析:
|
答案: (1)解:设P(a,0),Q(0,b) 则: 设M(x,y)∵ ∴ ∴ (2)解法一:设A(a,b), 则:直线SR的方程为: ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ① 对 ∴抛物线上S、R处的切线方程为:
联立②③,并解之得 故:B点在直线ax-2y-2b=0上 解法二:设A(a,b) 当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a) 与 设 则由韦达定理: 又过S、R点的切线方程分别为: 联立,并解之得 消去k,得:ax-2y-2b=0 故:B点在直线2ax-y-b=0上 |

练习册系列答案
相关题目
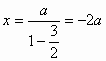

 ,即4y =(x1+x2)x-x1x2
,即4y =(x1+x2)x-x1x2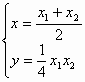 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
 (k为参数)
(k为参数)