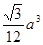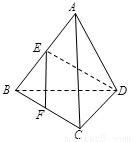题目内容
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFCH分别交 AB、BD、DC、CA于点E、F、G、H。
(1)判定四边形EFCH的形状,并说明理由;
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFCH?请给出证明。
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFCH?请给出证明。
解:(1)∵AD∥面EFGH,面ACD∩面EFGH=HC,
AD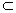 面ACD,
面ACD,
∴AD∥HG
同理EF∥HG,EH∥FG,
∴四边形EFCH是平行四边形,
∵三棱锥A-BCD是正三棱锥,
∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC
∴AD⊥BC
∴HG⊥EH
∴四边形EFGH是矩形;
(2)当 时,平面PBC⊥平面EFGH
时,平面PBC⊥平面EFGH
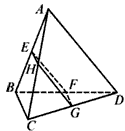
证明如下:作CP⊥AD于P点,连接BP,
∵AD⊥BC,
∴AD⊥面BCP
∵HG∥AD,
∴HC⊥面BCP,
∵HG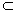 面EFCH,
面EFCH,
∴面BCP⊥面EFGH,
在Rt△APC中 ,∠CAP=30° ,AC=a,
∴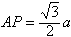 。
。
AD
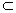 面ACD,
面ACD,∴AD∥HG
同理EF∥HG,EH∥FG,
∴四边形EFCH是平行四边形,
∵三棱锥A-BCD是正三棱锥,
∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC
∴AD⊥BC
∴HG⊥EH
∴四边形EFGH是矩形;
(2)当
 时,平面PBC⊥平面EFGH
时,平面PBC⊥平面EFGH证明如下:作CP⊥AD于P点,连接BP,
∵AD⊥BC,
∴AD⊥面BCP
∵HG∥AD,
∴HC⊥面BCP,
∵HG
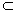 面EFCH,
面EFCH,∴面BCP⊥面EFGH,
在Rt△APC中 ,∠CAP=30° ,AC=a,
∴
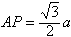 。
。
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
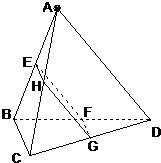 如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.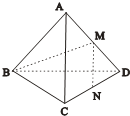 如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( )
如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( ) 如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是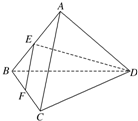 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是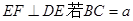 ,则A—BCD的体积为 ( )
,则A—BCD的体积为 ( )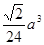 B.
B.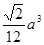
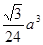 D.
D.