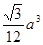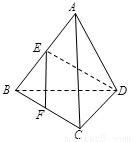题目内容
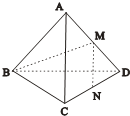 如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( )
如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( )分析:先证明AC⊥面BMD,进而可得AC⊥AD,连接AN,BN,则BN⊥CD,AN⊥CD,故∠ANB为正三棱锥的侧面与底面所成角,从而可求其正切值.
解答: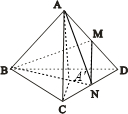 解:设点A在面BCD内的射影为A′
解:设点A在面BCD内的射影为A′
∵三棱锥A-BCD为正三棱锥
∴AB=AD,△BCD为正三角形,A′为△BCD中心
∴CD⊥BA′,∵AA′⊥面BCD
∴CD⊥AB,
∵M、N分别是AD、CD的中点
∴MN∥AC,
∵BM⊥MN,
∴AC⊥BM
又∵BD⊥平面ACA',BD?平面ACA'
∴AC⊥BD,
∵BD∩BM=B
∴AC⊥面BMD,
∵AD?面BMD
∴AC⊥AD
连接AN,BN,则BN⊥CD,AN⊥CD
∴∠ANB为正三棱锥的侧面与底面所成角
设CD=2a,则BN=
a,AN=a,AB=
a
∴∠BAN=90°
在△ABN中,tan∠ANB=
=
故选D.
 解:设点A在面BCD内的射影为A′
解:设点A在面BCD内的射影为A′∵三棱锥A-BCD为正三棱锥
∴AB=AD,△BCD为正三角形,A′为△BCD中心
∴CD⊥BA′,∵AA′⊥面BCD
∴CD⊥AB,
∵M、N分别是AD、CD的中点
∴MN∥AC,
∵BM⊥MN,
∴AC⊥BM
又∵BD⊥平面ACA',BD?平面ACA'
∴AC⊥BD,
∵BD∩BM=B
∴AC⊥面BMD,
∵AD?面BMD
∴AC⊥AD
连接AN,BN,则BN⊥CD,AN⊥CD
∴∠ANB为正三棱锥的侧面与底面所成角
设CD=2a,则BN=
| 3 |
| 2 |
∴∠BAN=90°
在△ABN中,tan∠ANB=
| ||
| a |
| 2 |
故选D.
点评:本题考查了正三棱锥的性质,二面角的求法和面面垂直的性质,解题时要有空间想象力,要能恰当的沟通未知量之间的关系,能够用转化的思想方法将空间问题化为平面问题

练习册系列答案
相关题目
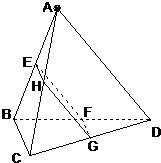 如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H. 如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是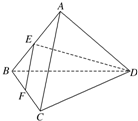 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是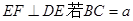 ,则A—BCD的体积为 ( )
,则A—BCD的体积为 ( )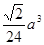 B.
B.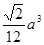
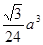 D.
D.