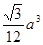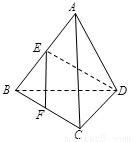题目内容
 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
| ||
| 24 |
| ||
| 24 |
分析:根据EF与DE的垂直关系,结合正棱锥的性质,判断三条侧棱互相垂直,再求得侧棱长,根据体积公式计算即可.
解答:解:∵E、F分别是AB、BC的中点,∴EF∥AC,又∵EF⊥DE,
∴AC⊥DE,
取BD的中点O,连接AO、CO,∵正三棱锥A-BCD,
∴AO⊥BD,CO⊥BD,∴BD⊥平面AOC,又AC?平面AOC,∴AC⊥BD,
又DE∩BD=D,∴AC⊥平面ABD;
∴AC⊥AB,
设AC=AB=AD=x,则x2+x2=1⇒x=
VC-ABD=
S△ABD•AC=
AB•AD•AC=
.
故答案是
∴AC⊥DE,
取BD的中点O,连接AO、CO,∵正三棱锥A-BCD,
∴AO⊥BD,CO⊥BD,∴BD⊥平面AOC,又AC?平面AOC,∴AC⊥BD,
又DE∩BD=D,∴AC⊥平面ABD;
∴AC⊥AB,
设AC=AB=AD=x,则x2+x2=1⇒x=
| ||
| 2 |
VC-ABD=
| 1 |
| 3 |
| 1 |
| 6 |
| ||
| 24 |
故答案是
| ||
| 24 |
点评:本题考查三棱锥的体积.V棱锥=
Sh.
| 1 |
| 3 |

练习册系列答案
相关题目
 如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.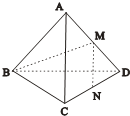 如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( )
如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( ) 如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是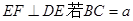 ,则A—BCD的体积为 ( )
,则A—BCD的体积为 ( )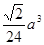 B.
B.
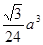 D.
D.