题目内容
(2012•宣城模拟)在平面直角坐标系下,已知 C1:
(t为参数,m≠0的常数),C2:
(θ为参数).则C1、C2位置关系为( )
|
|
分析:先把参数化为普通方程,利用直线恒过圆内点,我们就可以得出结论
解答:解:C1:
(t为参数,m≠0的常数),消去参数可得y=-
x+1;
C2:
(θ为参数),消去参数可得x2+y2=4
因为直线y=-
x+1恒过 P(0,1),它在圆内.
∴直线与圆恒相交
故选A
|
| 1 |
| m |
C2:
|
因为直线y=-
| 1 |
| m |
∴直线与圆恒相交
故选A
点评:本题考查参数方程,直线和圆的位置关系,过定点的直线系等知识,判断点在圆内是关键.

练习册系列答案
相关题目
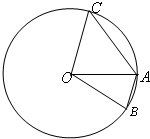 (2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则
(2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则