题目内容
(2012•宣城模拟)若变量x,y满足约束条件
,则z=2x+4y的最小值为( )
|
分析:作出不等式组所表示的平面区域,由z=2x+4y可得y=-
x+
z,则
z表示目标函数直线在y轴上的截距,截距越大,则z越大,作直线L:y=-
x,然后把直线L向可行域平移,结合图象判断取得最小值的位置,即可求解
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:作出不等式组所表示的平面区域,如图所示的四边形ABCD
由z=2x+4y可得y=-
x+
z,则
z表示目标函数直线在y轴上的截距,截距越大,则z越大
作直线L:y=-
x,然后把直线L向可行域平移,由题意可知,经过点B时,z最小,经过点C时,z最大
由
可得B(2,0),此时z=4
故选B

由z=2x+4y可得y=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
作直线L:y=-
| 1 |
| 2 |
由
|
故选B

点评:本题主要考查了线性规划知识的简单应用,解答本题的关键有两个:①要准确理解目标函数中z的几何意义②压迫准确判断目标函数经过可行域内点的先后顺序,判断的标准是把目标函数的直线斜率与边界直线的斜率进行比较

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
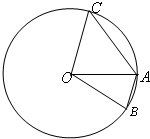 (2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则
(2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则